Calculating Charges q_1, q_2, and q_3 with Integration

[kyang002]

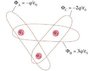
Question 4

What is the charge q_1?

What is the charge q_2?

What is the charge q_3?

Unsure of which equation to use, and the equations that I am looking at involve integration.

Φ = integral (E * dA) = EA sphere

Φ = q / ε

Can someone teach me how to do this problem?

 

[dextercioby]

HINT:Use the property of the electric flux (which is a scalar) of adding wrt the same surface.You'll have to solve a very simple system of equations...

Daniel.

 

[kyang002]

Property of Electric Flux = EA cos theta? But there is no theta. Unsure of the area and of the E.

 

[dextercioby]

No.Let be \Phi_{1} the electric flux generated by a charge q_{1} through the (closed) surface S.Similar \Phi_{2} for q_{2} [/itex].Then the total flux is simply the sum of Phi's which,due to the same denominator (epsilon),translates to the charges...

Daniel.

 

[kyang002]

So what is the charge of q_1, q_2, and q_3?

-q/E + (-2q/E) + 3q/E = 0/E = 0

The charge of each is 0?

 

[dextercioby]

No,you have to write equations of the type phi_{1}+phi_{2}=phi_{tot} for all 3 surfaces & will end up with an algebraic system of 3 eqn. with 3 unknowns,namely the charges.

Daniel.

 

[kyang002]

Okay, got it. The answers are 2q, q, -3q. Am I correct?