Calculating magnetic flux density using Biot-Savart law.

[3OPAH]

Hello, all. I have been working on the following problem and was wondering if someone could check my work and provide some valuable input:

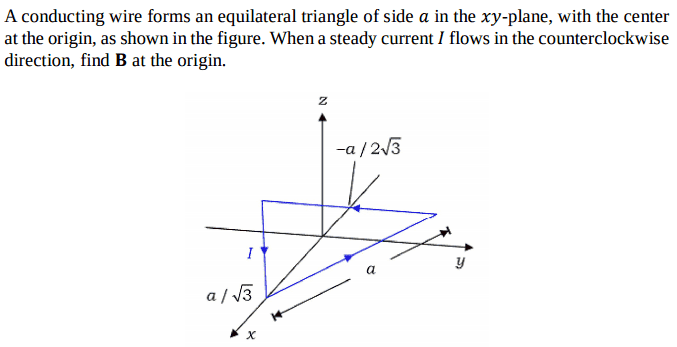
Here is my work:

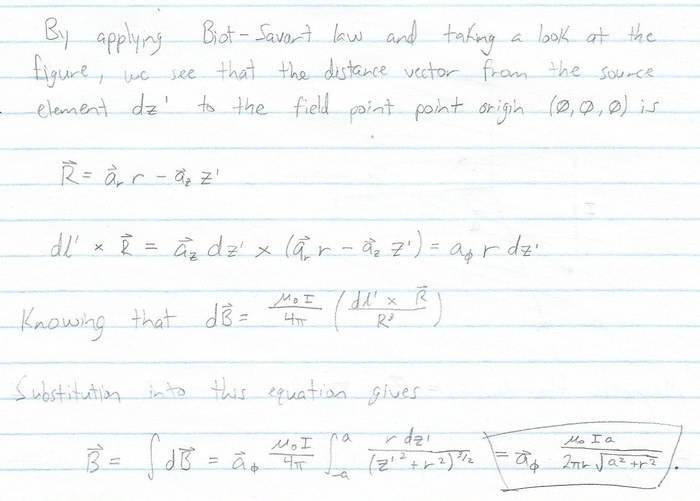
What do you guys think about my approach to this problem?

 

[mfb]

What is r, why do you consider z if everything happens in the x/y plane? Where does the expression for $\vec{R}$ come from?
In particular, how can your result depend on "r" which does not appear in the problem statement? The direction of the answer does not seem to make sense - how can something at the origin point in the direction of an angle?

Did you try to use cylindrical coordinates? I don't think that helps.

I don't understand why you integrate from -a to a.

I think you forgot to multiply the final result by 3 for the three wires, but there are several other things to fix first.

 

[3OPAH]

What is r, why do you consider z if everything happens in the x/y plane? Where does the expression for $\vec{R}$ come from?
In particular, how can your result depend on "r" which does not appear in the problem statement? The direction of the answer does not seem to make sense - how can something at the origin point in the direction of an angle?

Did you try to use cylindrical coordinates? I don't think that helps.

I don't understand why you integrate from -a to a.

I think you forgot to multiply the final result by 3 for the three wires, but there are several other things to fix first.

You are correct. Neither dl nor R should have components along e_z. Since the triangle lies in the x-y plane (z=0), dl should have components along e_x and e_y. Also, R should only have components along e_x and e_y because it's pointing from the location of dl , which is in the x-y plane, to the origin, which is also in the x-y plane. Accordingly, the cross product dl x R would come out to be along e_z, which is what we should expect from the right hand rule.

I am having a hard time computing dl and R. When I find dl and R it's a simple substitution into dB from there. Could you show me how you would calculate dl and R ?

 

[mfb]

Did you find the coordinates of the three corners? dl will be along one of the edges - there is an easy one and two more complicated edges. R follows from the choice of the edge. Note that it varies along the length of the wire.