magnifik
- 350
- 0
I need help finding the thevenin equivalent voltage for the following network:
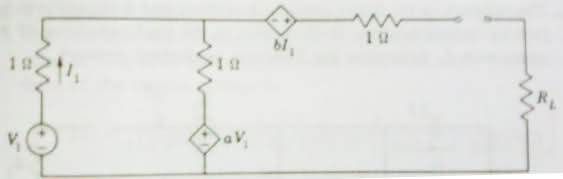
i did source transformations so that i could analyze it using the node voltage method.

my equations are:
I1 = v1
(a) vx + vx - vT = v1 + av1 - bv1
2vx - vT = v1 + av1 - bv1
(b) vT - vx + vT = bv1
2vT - vx = bv1
when i simplify (by substituting vx), i get
vT = v1/3(a + b + 1)
however, the answer should be
vT = v1/2(a + b + 1 - ab)
help please! thanks.
i did source transformations so that i could analyze it using the node voltage method.
my equations are:
I1 = v1
(a) vx + vx - vT = v1 + av1 - bv1
2vx - vT = v1 + av1 - bv1
(b) vT - vx + vT = bv1
2vT - vx = bv1
when i simplify (by substituting vx), i get
vT = v1/3(a + b + 1)
however, the answer should be
vT = v1/2(a + b + 1 - ab)
help please! thanks.
Last edited: