Can I determine the phase angle of this equation by using the sin function?

[nuclearfireball_42]

Homework Statement

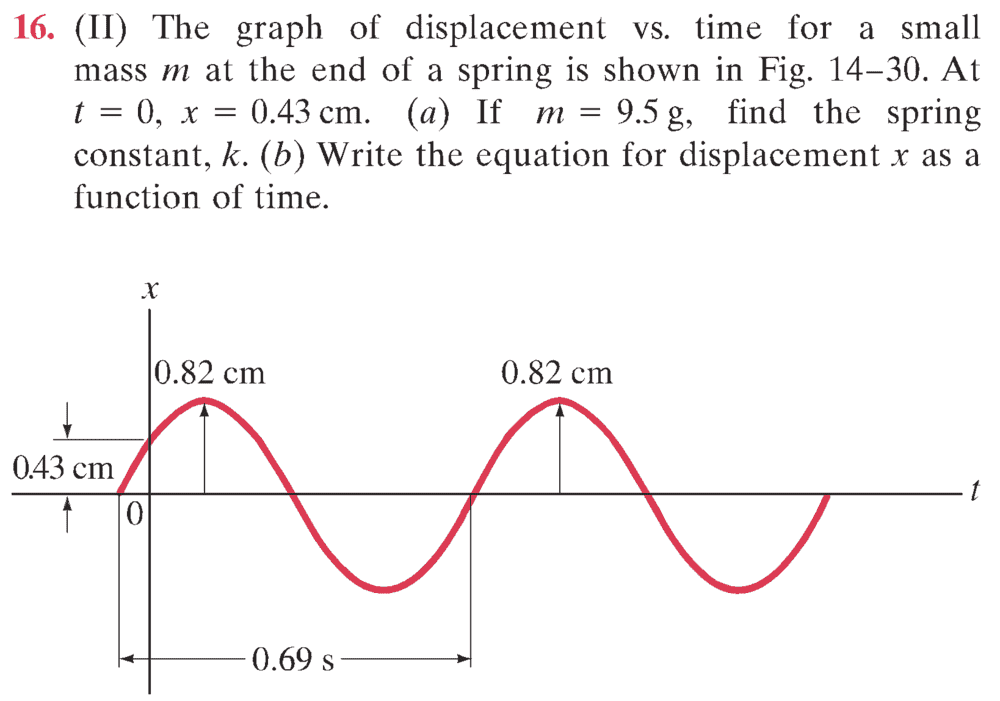
The graph of displacement vs time for a small mass m at the end of a spring is shown in Fig. 14-30. At t = 0, x = 0.43 cm.
(a) If m = 9.5 g, find the spring constant, k.
(b) Write the equation for displacement x as a function of time.

Relevant Equations

x(t) = Asin(ωt + φ)

x(t) = Acos(ωt - φ)

I've got the answer for (a). It's k = 0.78 N/m.

I'm having problems with (b). I know that the equation of displacement in this case should either be :

x(t) = Asin(ωt + φ)

or

x(t) = Acos(ωt - φ)

where A = amplitudeFrom what I understand, both the equation above should give the same result as the sine and cosine functions are the reason for the different signs before the phase angle. But the author of the book wrote the second equation (the one with the cos function) to be the answer. Thinking that my answer which is in the form of the first equation could just be an alternative of the second, I checked the result of the functions numerically and I found them to be different . Is it something to do with my calculation or is my understanding just wrong?

The picture of the graph :

 

[PeroK]

Your understanding is correct, so you must have made a mistake in the calculations. Note that:
$$\sin(x + \frac {\pi}{2}) = \cos(x)$$
Hence, any sine or cosine function can always be written either way with a different phase.

 

[nuclearfireball_42]

Your understanding is correct, so you must have made a mistake in the calculations. Note that:
$$\sin(x + \frac {\pi}{2}) = \cos(x)$$
Hence, any sine or cosine function can always be written either way with a different phase.

This might be a dumb question but I have to calculate in radians mode in the calculator right to find x?

 

[PeroK]

This might be a dumb question but I have to calculate in radians mode in the calculator right to find x?

Always in radians for SHM.

 

[haruspex]

This might be a dumb question but I have to calculate in radians mode in the calculator right to find x?

In solving the SHM differential equation, use is made of the standard equations $\frac{d\sin(x)}{dx}=\cos(x)$ etc. Those equations are only valid in radians. If working in degrees you would have to include a constant factor.

 

[Merlin3189]

... both equations should give the same result, as the sine and cosine functions are the reason for the different signs before the phase angle. ... author of the book wrote the second equation (the one with the cos function) to be the answer. Thinking that my answer which is in the form of the first equation could just be an alternative of the second, I checked the result of the functions numerically and I found them to be different . Is it something to do with my calculation...

If you show your calculations, we might be able to tell.
When you use sin instead of cos, the magnitude of the phase will usually change, not just the sign.