SpaceIsCool
- 6
- 1
Homework Statement
We solved the differential equation (2.29),
and integrate both sides from time 0 to
Homework Equations
The Attempt at a Solution
Integrate both sides of the separated form of the differential equation from time 0 to t and then write
Attachments
-
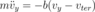 3jQQorlME_t__2tW6a8kcnYMlu3IQt04D8vDrtjBPfupq1HsNrmZUl4xD1bMqDKY3ssnC-gk-e0sg9TyVu5zgFWU6VsDs5dw.png5.7 KB · Views: 716
3jQQorlME_t__2tW6a8kcnYMlu3IQt04D8vDrtjBPfupq1HsNrmZUl4xD1bMqDKY3ssnC-gk-e0sg9TyVu5zgFWU6VsDs5dw.png5.7 KB · Views: 716 -
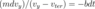 XX1f9LT1V4iwLFhOj0k17drHhyTjkFlbPurmlbw2iveZyOY70N-4lnsJ8nUSC3cy-BfGiq8hJ43C7kc4ynZMgcGMLMb88cfc.png5.8 KB · Views: 580
XX1f9LT1V4iwLFhOj0k17drHhyTjkFlbPurmlbw2iveZyOY70N-4lnsJ8nUSC3cy-BfGiq8hJ43C7kc4ynZMgcGMLMb88cfc.png5.8 KB · Views: 580 -
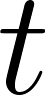 hFE8d86mE5qF60vFSYngvVUpWFO68N1uVz5xGeu-sdHjYX8yyDs4qyalPiGohlD-DzZB5cO0NK1No--OW9J5HFcXei2jS3kR.png508 bytes · Views: 585
hFE8d86mE5qF60vFSYngvVUpWFO68N1uVz5xGeu-sdHjYX8yyDs4qyalPiGohlD-DzZB5cO0NK1No--OW9J5HFcXei2jS3kR.png508 bytes · Views: 585 -
 G2YEY28crCFfirUT4r7rOHNBaqxt3skHs4ekGyy7QIkYNYJMb9qQRwnt8Y4FDIwi7g143bzRjZdRbStBbwEfDVbrHMPtZ2wq.png1.2 KB · Views: 545
G2YEY28crCFfirUT4r7rOHNBaqxt3skHs4ekGyy7QIkYNYJMb9qQRwnt8Y4FDIwi7g143bzRjZdRbStBbwEfDVbrHMPtZ2wq.png1.2 KB · Views: 545 -
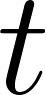 8O4uKQnrmKWgR9UXYtK_PW1xcKLsdhnUg2degFW--u1CO84TGSRm2KcGLfcbAWyOdelH6M3yuu9tGdKH2IV5ExkbePnjzWzD.png508 bytes · Views: 554
8O4uKQnrmKWgR9UXYtK_PW1xcKLsdhnUg2degFW--u1CO84TGSRm2KcGLfcbAWyOdelH6M3yuu9tGdKH2IV5ExkbePnjzWzD.png508 bytes · Views: 554 -
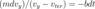 XX1f9LT1V4iwLFhOj0k17drHhyTjkFlbPurmlbw2iveZyOY70N-4lnsJ8nUSC3cy-BfGiq8hJ43C7kc4ynZMgcGMLMb88cfc.png5.8 KB · Views: 577
XX1f9LT1V4iwLFhOj0k17drHhyTjkFlbPurmlbw2iveZyOY70N-4lnsJ8nUSC3cy-BfGiq8hJ43C7kc4ynZMgcGMLMb88cfc.png5.8 KB · Views: 577 -
 5QaZ9UrgA6wAB6mhn4OqOWzSES5iMKWq5HeIyNUGso3ndh-iMCdNLtkStb_BTCMFG1FJftZiANbli2Zo348uSWuMx19EXBa9.png4.9 KB · Views: 586
5QaZ9UrgA6wAB6mhn4OqOWzSES5iMKWq5HeIyNUGso3ndh-iMCdNLtkStb_BTCMFG1FJftZiANbli2Zo348uSWuMx19EXBa9.png4.9 KB · Views: 586 -
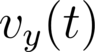 FNV42vu_LJT7kC0fuNcaHis6ixZXlVrOAWtlALmrPOaeDAfRi_eI6YIiiGtmYj4_vUbVjdFCqhOINDnhpPXX6F29AvH3d_5M.png2.6 KB · Views: 606
FNV42vu_LJT7kC0fuNcaHis6ixZXlVrOAWtlALmrPOaeDAfRi_eI6YIiiGtmYj4_vUbVjdFCqhOINDnhpPXX6F29AvH3d_5M.png2.6 KB · Views: 606 -
 5QaZ9UrgA6wAB6mhn4OqOWzSES5iMKWq5HeIyNUGso3ndh-iMCdNLtkStb_BTCMFG1FJftZiANbli2Zo348uSWuMx19EXBa9.png4.9 KB · Views: 619
5QaZ9UrgA6wAB6mhn4OqOWzSES5iMKWq5HeIyNUGso3ndh-iMCdNLtkStb_BTCMFG1FJftZiANbli2Zo348uSWuMx19EXBa9.png4.9 KB · Views: 619 -
 AATrdWCxsgaZiMrK_EVvJA8r04k2mPrRD1RkRyOQjLMBfO8Jfd-cB-T9FosAtd6RnF_lwC5ufVhlxA1bD43bwv94WCNop01A.png6.3 KB · Views: 581
AATrdWCxsgaZiMrK_EVvJA8r04k2mPrRD1RkRyOQjLMBfO8Jfd-cB-T9FosAtd6RnF_lwC5ufVhlxA1bD43bwv94WCNop01A.png6.3 KB · Views: 581 -
 uVh4fi89LFMNhydQFiEj8Zqg5PcabxW1p9-KV6nFoYOPqGd4OFBd8OASdAY4nJzF3TsXecQhJvXOE85om7SsDJ8T7SuvcY7F.png5.8 KB · Views: 628
uVh4fi89LFMNhydQFiEj8Zqg5PcabxW1p9-KV6nFoYOPqGd4OFBd8OASdAY4nJzF3TsXecQhJvXOE85om7SsDJ8T7SuvcY7F.png5.8 KB · Views: 628