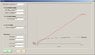
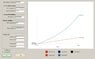
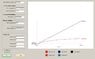
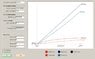
Now that I am working the Van der Waals case, that Pv term is coming back to bite me. There is no easy way to get it in ##T_{in}## terms. But cannot I simply use the initial conditions for ##(Pv)_{in}## and then let the solution for ##T_f## be an input into the EOS to get tank pressure, then use that tank pressure as the reference for my change in inlet pressure? Since I am making the assumption that since the mole rate into the tank is constant, then the inlet pressure is always a constant ##\Delta P## over the tank pressure? But it seems that does not take into account the changes in inlet pressure between each iteration. Between each mole "chunk" I add to the tank at each iteration, there has been a continuous change in tank and inlet pressures between the moment of the last chunk, and the current one. In that case, it looks like another integral is involved.