Cantilever equilibrium problem

[UMath1]

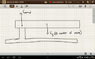
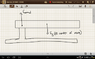
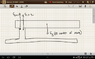
I am trying to resolve for the forces in the attached diagram. In order for this object to be in rotational equilibrium, the torques of the normal force and the garvitational force would have to be equal. However, this would imply that normal force produced by the fulcrum would be far greater than force of gravity at center of mass. The problem is that for an object to be in mechanical equilibrium, the forces must also be equal. So how can both of these be true? The other issue I am having is that you are allowed to find torques using any axis. If that is true and I set the axis of rotation to be the point of contact with the fulcrum, then there will be a net non zero torque. So how is this situation pssible?

 

[Dale]

So at the attachment of a cantilever beam there is a torque as well as a net force. Without that additional torque, as you mention, there is no static solution. For example, if you attach with a hinge instead of a cantilever then the beam will fall until it hangs below the hinge.

 

[UMath1]

But then, if a net force is present, how is it possible for the beam to remain in translational equilibrium?

 

[Dale]

If it is in equilibrium then there is no net force and no net torque.

$F_{normal }=-F_{g}$

 

[UMath1]

So at the attachment of a cantilever beam there is a torque as well as a net force.

Then that means that there is a net force on the beam. But the beam is in static equilibrium and for that to be the case there cannot be a net torque or net force.

 

[Dale]

Sorry, my words are confusing. The net force on the beam is 0. The force at the cantilever attachment is non zero.

 

[UMath1]

So then if the forces are equivalent, how then can the torques be equal? The normal force has a smaller lever arm than the gravitational force.

 

[Dale]

So then if the forces are equivalent, how then can the torques be equal? The normal force has a smaller lever arm than the gravitational force.

A cantilever attachment also supports a torque (aka bending moment). There are other attachments, like a hinge, that do not support a torque. Think of what would happen if you tried to attach a cantilever beam using a hinge. Clearly, that shows that there is a torque at the attachment.

 

[UMath1]

I am not sure I understand what you mean. But it seems to me that unless a third force is present the conditions for both translational and rotational equilibrium cannot be met. Would this be a more correct diagram?

 

[Dale]

Usually it is just represented as a torque at the attachment rather than a second force. But yes, the basic idea is that you need an additional degree of freedom in your free body diagram.

 

[UMath1]

What I don't understand though is that it should require less normal force if the fulcrum were placed at the center of mass. However, for translational equilibrium to hold Fn=-Fg

 

[Dale]

It would require the same normal force. It would require less torque.

 

[UMath1]

But the torque produced by gravity would have to be constant as both the center of mass and the weight of the object would have to be constant. So if gravity's torque is constant, the torque produced from the normal force would have to be constant too in order for the object to be in rotational equilibrium.

 

[Dale]

There is the torque from the normal force, but in addition there is also a torque from the bending moment at the attachment point. You have to account for both. The torque produced from gravity, the torque from the normal force, and the additional torque at the attachment must sum to zero.

 

[UMath1]

What is the additional torque produced by? How would you describe the additional force?

 

[Dale]

The additional torque is produced by the attachment. In order for the beam to qualify as a "cantilever" it must, by definition, have an attachment which supports additional torque.

You didn't specify the construction of the cantilever, but for example, suppose that the beam is welded in place, then the additional torque would be produced by the metal of the weld.

 

[UMath1]

I am still having issues with this. When I put in actual numbers I still end up having a net force or net torque. Can you see my work?

 

[Dale]

So again, I would not treat it as two forces. I would follow the standard practice of treating it as a force and a torque. If you do that then the force is clearly equal to $-F_g$. The torque can then be calculated by setting the axis at the normal force and calculating the opposite of the torque due to gravity.

However, if you do choose to represent it as two forces rather than a force and a torque, you can still solve it. First, look at how you have drawn it. Think about the torques produced by each force. Can you see that one of the two forces must point downwards? Can you tell which one?

 

[UMath1]

Is this how it should be?

 

[Dale]

Yes. That is the right idea, but I think your numbers are off.

 

[UMath1]

Yes. That is the right idea, but I think your numbers are off.

How so? Also, what if the weld were attached between the normal force and the center mass? How do we know where the weld would be attached?

 

[Dale]

It looks like the distance from $F_{normal}$ to $F_{weld}$ is 1 m and the distance from $F_{normal}$ to $F_g$ is 4 m. So the weld force should be 4 times the gravitational force.

As far as where it is, as I told you several times already, the usual approach is to consider the attachment to be a force and a torque instead of two forces. The ambiguity of the location of the force is one reason for adopting the practice.

 

[UMath1]

I don't understand how that would work though. If I set the attachment to be one force I run into the problem where only one of the two conditions for rotational equilibrium can be met. Am I not understanding something?

 

[Dale]

If I set the attachment to be one force I run into the problem where only one of the two conditions for rotational equilibrium can be met.

One force AND one torque. I have said this four times already!

 

[UMath1]

One force AND one torque.

I don't understand. I only have one torque coming from the attachment. Multiple torques would only be possible if there were multiple forces.

 

[UMath1]

The one force would be the net force at the point if attachment and the one torque would be the torque produced by that net force is how I understand it. Am I missing something?

 

[Dale]

Consider the axis through the point of attachment. The net force produces no torque about that axis. And yet there is a torque. This torque is separate from the net force. It is it's own independent torque.

 

[UMath1]

Torque is F x R. How can a torque be produced without a force. And if its on the axis of rotation, like you said, how can it exist? The lever arm would be 0.

 

[Dale]

Do you understand the concept of a limit? If so, then consider a finite torque to be the limit of two equal and opposite forces as the lever arm goes to 0 and the forces become infinite.

In reality, no force is ever applied at a point. There is always some finite region of contact over which some finite pressure is exerted. However, if that region of contact is small enough that we don't care about the difference from one end to the other, then we can simply ignore it and consider the force to be acting at a single point. Thus, a point force is the limit of a distributed force as the area goes to 0 and the pressure becomes infinite.

The point torque is the same kind of abstraction that you have already been using for forces.

 

[UMath1]

Which two forces? Normal and Attachment? And would this be the sum of the two forces?