PhotonTrail
- 13
- 0
Homework Statement
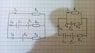
I'm not sure how to put this in words, but I shall try. Alternatively, I've attached an image. It's hand-drawn, but I hope it's legible enough.
Imagine a circuit drawn in the shape of a rectangle, with a single resistor ##R_1## on the top side, plus a DC cell ##\epsilon_2## and a second resistor ##R_3## on the bottom side. Now connect the left and right sides of the rectangle with a horizontal line in the middle. This portion of the circuit contains the following: a capacitor ##C_1##, a second DC cell ##\epsilon_1##, and a third resistor ##R_2##.
Question: What are the currents at every point in the circuit?
Homework Equations
None.
The Attempt at a Solution
I would say that the portion of the circuit with the capacitor has no current flowing through, i.e. ##I_2=0##. I originally thought too that ##I_1## and ##I_3## are equal to zero too, because I found it difficult to accept that there will be current flowing in the other parts of the circuit if there is no potential difference across the middle branch.
Am I mistaken in thinking that ##I_2## is zero? If I am not, am I wrong in assuming that the potential difference between the left and right sides of the middle branch is zero? If I am still not, then why do the top and bottom branches have currents flowing? How do the potential differences work out?
Many thanks for any assistance!