DavidDishere
- 12
- 0
Homework Statement
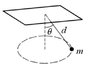
Consider a conical pendulum that consists of a bob
on one end of a string of negligible mass with the other end of the
string attached to a point on the ceiling, as shown. Given the proper
push, this pendulum can swing in a circle at a given angle, maintaining
the same distance from the ceiling throughout its swing. If the mass of
the bob is , the length of the string is d, and the angle at which it
swings is θ, what is the speed (v) of the mass as it swings? [Hint: Find
the vertical and inward radial components of the string’s tension.]
Homework Equations
FR = (mv2)/r
The Attempt at a Solution
For \SigmaFy I got FT = mg/cos θ
I said r = dsinθ
And for \SigmaFR I got FTdsin2 θ = v2
Plug in mg/cos θ for FT and sqrt(gd tanθ sin θ)= v
Is that right?