caesium
- 1
- 0
- Homework Statement
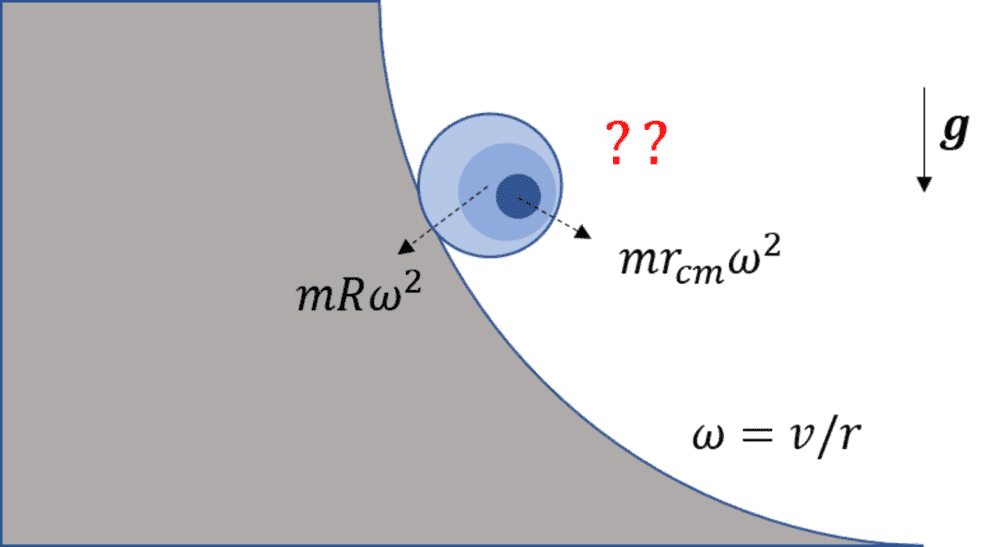
- Let's say we have a cylinder of radius r with non-uniform density, resulting in a center of mass shifted away from center of geometry. Let's assume that this center of mass mid-way between center and circumference. So, r_cm = r/2.
Now, let's say this cylinder is rolling down on a curved path of radius R + r. Assume no slip condition.
What is the centripetal force on this cylinder? Does it have "two centripetal forces", from which we find a resultant?
- Relevant Equations
- There are no equations here.
My initial attempt: Total Centripetal force on the cylinder would be given by $$\textbf{F}_{net} = mR\omega^2 \textbf{e}_1+mr_{cm}\omega^2 \textbf{e}_2$$ where the vectors e_1 and e_2 have magnitude 1 and point radially outwards (and continuously changing as the cylinder rolls down) as marked in the sketch below. Please advise. Thank you.