Tommie Robinson
- 6
- 1
Homework Statement
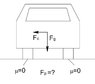
Find the speed at which a car of mass M will lose contact with the frictionless road
Homework Equations
Centripetal/Centrifugal forces (maybe?)
The Attempt at a Solution
I used OneNote to attempt this problem[/B]
https://onenote.com/webapp/pages?to...0EkvVRJz3ZRVraisuhYOUH0&id=636551577043927699
Attachments
Last edited by a moderator: