Ashshahril
- 4
- 1
- Homework Statement
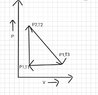
- What is the change in heat and internal energy in this PV diagram (attached link) from T2 to T3 (T represents temperature)?
- Relevant Equations
- ΔQ=mC(T3-T1)
Δu=ΔQ + Δw
ΔQ=mC(T3-T1)
But, will this C be Cp or Cv. Both pressure and volume changes. So, neither of them can be.
Feeling so confused
But, will this C be Cp or Cv. Both pressure and volume changes. So, neither of them can be.
Feeling so confused