neshepard
- 67
- 0
Homework Statement
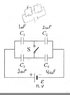
C. What is the charge on each of the four capacitors if switch S is closed? I have the charges if the switch is open, C1 and C2 are 8μC and C3 and C4 are 6μC since charges are same on series.
Homework Equations
The Attempt at a Solution
I know to find Ceq and work backwards, and that voltage in parallel is the same. But what happens to the volatage's and charges in both a series and parallel layout?
C1 and C3 are parallel Ceq=4μF
C2 and C4 are parallel Ceq=6μF
Each parallel group is in series.