jisbon
- 475
- 30
- Homework Statement
- -
- Relevant Equations
- -
Hi all,
Checking my answers here as it doesn't seem to match with the answers given to me. Would appreciate if anyone could point out the mistakes I made.
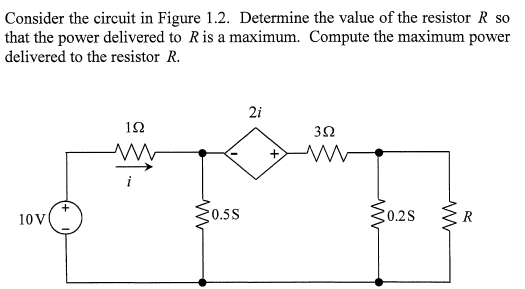
First I will compute Rth. Offing all independent sources, applying a known voltage across R (in this case 1v) and using mesh analysis,
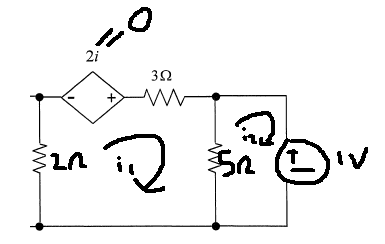
2i1+0 (since i =0) + 3i1+5(i1-i2) = 0
10i1=5i2
5i1=2.5i2 -- Equation 1
2nd Loop:
5(i2-i1)+1 =0
Combing this with equation 1,
5i2 - 2.5i2 +1 =0
i2 = -0.4A
Hence Rth = 1/0.4 = 2.5 ohms.
Note: For Rth, the answer stated was 1.92ohms using nodal analysis.
Now to find Vth, I will just use normal mesh analysis for the normal circuit:
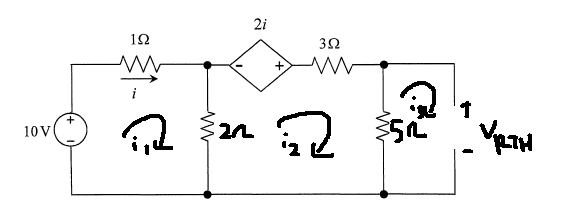
Mesh 1:
=-10+i1+2(i1-i2)=0 --> -10+3i1-2i2=0 --> **2i2 = 10+3i1**
Mesh 2:
2(i2-i1) - 2i1 +3i2+5(i2-i3) =0 --> **i1 = (-10i2+5i3)/4**
Mesh 3:
5(i3-i2)+Vr= 0 --> Vr= 5i2-5i3
Around whole loop:
=-10+i1-2i1+3i2+Vr=0 --> Using Mesh 3 equation, **i1=8i2-5i3-10**
Solving these 3 equations, i3 = 0.5A, i2 = 1.25A
Hence Vrth = 5( 1.25- 0.5) = 3.75V
Pmax =(Vrth^2)/4Rth = 1.40W?
Thanks.
Checking my answers here as it doesn't seem to match with the answers given to me. Would appreciate if anyone could point out the mistakes I made.
First I will compute Rth. Offing all independent sources, applying a known voltage across R (in this case 1v) and using mesh analysis,
2i1+0 (since i =0) + 3i1+5(i1-i2) = 0
10i1=5i2
5i1=2.5i2 -- Equation 1
2nd Loop:
5(i2-i1)+1 =0
Combing this with equation 1,
5i2 - 2.5i2 +1 =0
i2 = -0.4A
Hence Rth = 1/0.4 = 2.5 ohms.
Note: For Rth, the answer stated was 1.92ohms using nodal analysis.
Now to find Vth, I will just use normal mesh analysis for the normal circuit:
Mesh 1:
=-10+i1+2(i1-i2)=0 --> -10+3i1-2i2=0 --> **2i2 = 10+3i1**
Mesh 2:
2(i2-i1) - 2i1 +3i2+5(i2-i3) =0 --> **i1 = (-10i2+5i3)/4**
Mesh 3:
5(i3-i2)+Vr= 0 --> Vr= 5i2-5i3
Around whole loop:
=-10+i1-2i1+3i2+Vr=0 --> Using Mesh 3 equation, **i1=8i2-5i3-10**
Solving these 3 equations, i3 = 0.5A, i2 = 1.25A
Hence Vrth = 5( 1.25- 0.5) = 3.75V
Pmax =(Vrth^2)/4Rth = 1.40W?
Thanks.