Conceptual question on heat transfer (Steady-state)

[batmankiller]

So this isn't a homework problem persay, it was given information but I just couldn't wrap my head on why this was true.

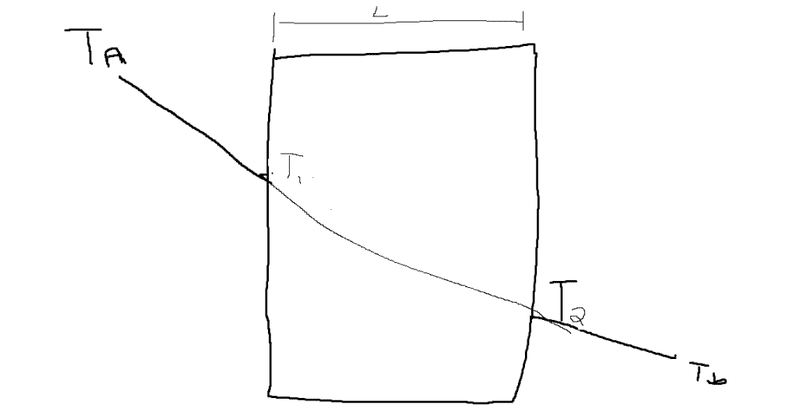
We have 1-d heat transfer through a planar slab. If we have a T_a for the temperature outside, then as we T_1 for the temperature on one end of the surface, and T_2 for the temperature on the other end, and T_b as the temperature outside the building on the other, how can we tell that this is a steady state problem?

h is the material thermal convection constant and k is the material thermal conductivity
We eventually set the convection flux equal to the conduction flux:

J_conduction = J_convection =
h(T_h - T_1) = (K/L)(T_1 -T_3)

Why is he able to set the fluxes equal to each other? Why wouldn't the convection flux be different from the conduction flux? Perhaps this would be more clear if someone could use an analogy approach of electrical circuits?

 

[gneill]

The variables in your equation don't seem to match the labels in your diagram.

 

[batmankiller]

Yes sorry T_3 is T_2. and T_h is T_A.

 

[gneill]

If you want an electrical analogy, the convection and thermal conductivity constants become electrical conductivities. As such they will support potential differences when current flows through them. Stated another way, a potential difference across them causes a current to flow through them. Thus heat transfer is modeled as an electric current.

To model your diagram as an electric circuit, the temperatures become voltages, the heat flow becomes current. The convection constant applies at the interfaces and the conductivity applies to the bulk slab. Assuming Ta > Tb, heat will flow from Ta towards Tb. It flows sequentially from the medium at Ta to the slab via the left interface, through the body of the slab to the right interface and hence to the medium at Tb. As such it is modeled as a series circuit:

It should be noted that the constants h and k should really be multiplied by the cross sectional area, as they represent conductivity per unit area. Not represented in the diagram is the thermal mass of the slab (which would be represented as a capacitance). At steady state (after a long time at constant conditions) such a capacitance reaches a final "charge" and ceases to affect circuit operation, so the diagram represents steady state conditions.

At steady state the current must be the same all along its path, otherwise electrons (or heat) would be piling up in some places or running deficits in others -- creating spontaneous charge buildups or deficits (hot or cold spots) contrary to the laws of thermodynamics.

 

[batmankiller]

Ah that makes a lot of sense. Quick question though, is the heat flux equivalent to the J in electric flux as well?

 

[gneill]

Ah that makes a lot of sense. Quick question though, is the heat flux equivalent to the J in electric flux as well?

There are several different ways to model various physical system electrically, equating different quantities to either voltage or current. In this case temperature is modeled as voltage and heat flow (Watts) is modeled as current J. But it would be possible to use current density, such as in a conductor of a given size, or current flux. One has to ponder the underlying makeup of the various constants between physical systems to keep things consistent