bill.connelly
- 21
- 0
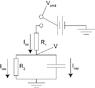
I'm trying to wrap me head around what should be a very simple system, but I just can't manage it. I know there is no closed form for this problem (ignoring a voltage step like is shown in the diagram below, imagine it is a arbitrary voltage supply, or even more exactly, that R2 changes over time), and that to solve it I need to convolve equations (though I would hope I could do a pretty good numerical approximation too).

What I'm trying to do is get the equation for dV/dt in terms of Vcmd, R1, R2 and C
So I know
Itot = Ires + Icap
Itot = V/R2 + C * dV/dt
I also know V = Vcmd - Itot*R1
Itot = (Vcmd-V)/R1
Therefore
(Vcmd-V)/R1 = V/R2 + C * dV/dt
rearranging gives
C*dV/dt = (Vcmd-V)/R1 - V/R
I like that, because it means as R1 drops to zero, dV/dt approaches infinity (which is what I would expect, i.e. V should approach Vcmd instantly) BUT if R1 did drop to zero, and V = Vcmd, dV/dt should be zero, right? But that equation says otherwise. Likewise, as R1 approaches infinity, I would have thought dV/dt would approach zero.
Am I doing something wrong here? Making an invalid assumption?
What I'm trying to do is get the equation for dV/dt in terms of Vcmd, R1, R2 and C
So I know
Itot = Ires + Icap
Itot = V/R2 + C * dV/dt
I also know V = Vcmd - Itot*R1
Itot = (Vcmd-V)/R1
Therefore
(Vcmd-V)/R1 = V/R2 + C * dV/dt
rearranging gives
C*dV/dt = (Vcmd-V)/R1 - V/R
I like that, because it means as R1 drops to zero, dV/dt approaches infinity (which is what I would expect, i.e. V should approach Vcmd instantly) BUT if R1 did drop to zero, and V = Vcmd, dV/dt should be zero, right? But that equation says otherwise. Likewise, as R1 approaches infinity, I would have thought dV/dt would approach zero.
Am I doing something wrong here? Making an invalid assumption?