tjholi
- 3
- 0
- Homework Statement
- I am having trouble deriving the expression from the initial equations. (Calculate the emptying time considering Volume conservation)
- Relevant Equations
- Q=A*sqrt(b(H-h(t)) And we have dh/dt =Q/S (conservation equation) and we have to obtain h/H = 1-(1-t/te)^2 with te= (2S/A*)(H/b)^1/2
Problem Statement: I am having trouble deriving the expression from the initial equations. (Calculate the emptying time considering Volume conservation)
Relevant Equations: Q=A*sqrt(b(H-h(t)) And we have dh/dt =Q/S (conservation equation) and we have to obtain h/H = 1-(1-t/te)^2 with te= (2S/A*)(H/b)^1/2
I know this is solving a 1st order ODE but I am lost at rearranging prior to solving.
This is not to be submitted, I am revising for an exam)
Thanks for your help
J
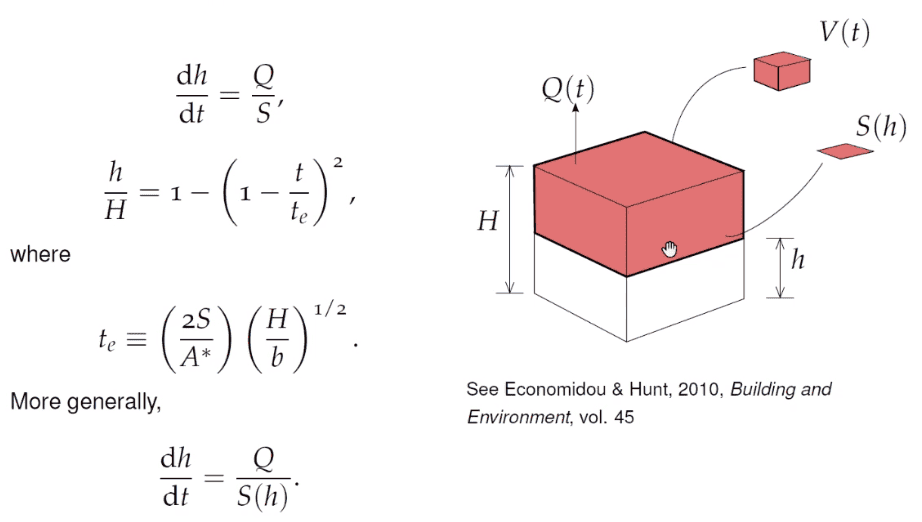
Relevant Equations: Q=A*sqrt(b(H-h(t)) And we have dh/dt =Q/S (conservation equation) and we have to obtain h/H = 1-(1-t/te)^2 with te= (2S/A*)(H/b)^1/2
I know this is solving a 1st order ODE but I am lost at rearranging prior to solving.
This is not to be submitted, I am revising for an exam)
Thanks for your help
J