Crystal
- 4
- 0
Poster has been warned about posting with no effort shown
Homework Statement
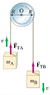
Two masses, mA = 40.0 kg and mB = 55.0 kg, are connected by a massless cord that passes
over a pulley that is free to rotate about a fixed axis. This device is known as an
Atwood’s Machine. The pulley is a solid cylinder of radius R = 0.360 m and mass of 7.50
kg.
1. Determine the linear acceleration of the two masses
2. Determine the angular acceleration of the pulley
Homework Equations
a=atan+ar
The Attempt at a Solution
not sure how to start, any hints would be great