zenterix
- 774
- 84
- Homework Statement
- Determine the Thevenin equivalent of the circuit below.
- Relevant Equations
- ##V=iR##
Here is the circuit that we need to find the Thevenin equivalent of
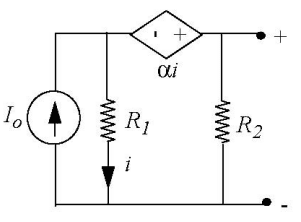
I am really not confident that the attempted solution below is correct.
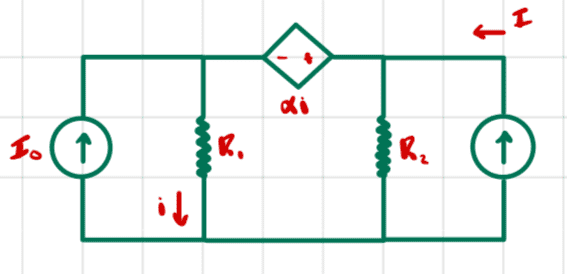
Let's put a test current source between the terminals we're interested in
First let's compute the open circuit voltage. We set the newly introduced test current source to zero and compute the voltage between the terminals.
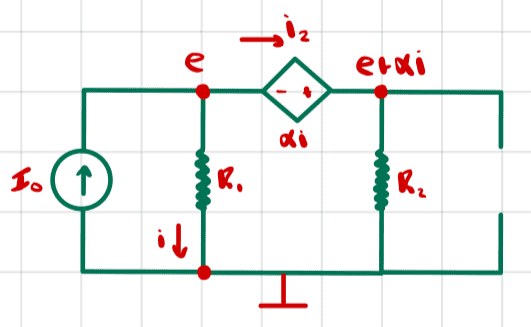
We have three unknowns ##e, i,## and ##i_2##.
We have three equations
$$I_0=i+i_2\tag{1}$$
$$i_2=\frac{e+\alpha i}{R_2}\tag{2}$$
$$i=\frac{e}{R_1}\tag{3}$$
Sub (3) into (2) to obtain
$$i_2=\frac{e(R_1+\alpha R_2)}{R_1R_2}\tag{4}$$
Now sub (2) and (4) into (1) and solve for ##e## to obtain
$$e=\frac{R_1R_2I_0}{R_1+R_2+\alpha}\tag{5}$$
Then
$$i=\frac{e}{R_1}=\frac{R_2I_0}{R_1+R_2+\alpha}\tag{6}$$
The open-circuit voltage is ##e+\alpha i## and this is
$$V_{oc}=e+\alpha i=\frac{R_2(\alpha+R_1)}{R_1+R_2+\alpha}I_0\tag{7}$$
Next, we set current source ##I_0## to zero and we solve for the voltage on the terminals we're interested in.
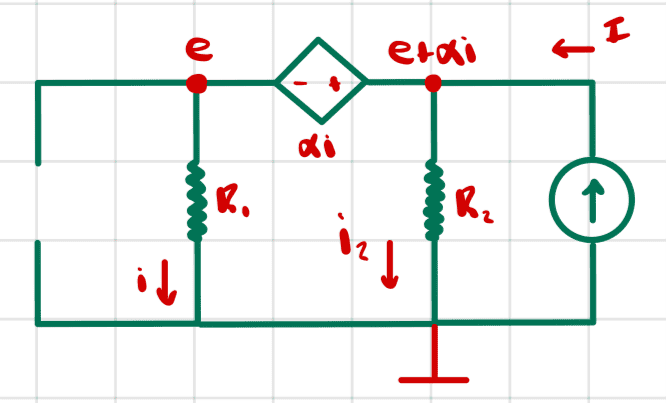
We have the same three unknowns as before, and the equations turn out to be the same as before except that instead of ##I_0## we have ##I## in the equations.
Thus, for this subcircuit we have
$$V_b=e+\alpha i=\frac{R_2(\alpha+R_1)}{R_1+R_2+\alpha}I\tag{8}$$
The Thevenin equivalent resistance is
$$R_{eq}=\frac{R_2(\alpha+R_1)}{R_1+R_2+\alpha}\tag{9}$$
By superposition, the voltage at the terminals of the original circuit is
$$V=V_{oc}+V_b=\frac{R_2(\alpha+R_1)}{R_1+R_2+\alpha}(I+I_0)\tag{10}$$
The Thevenin equivalent circuit is
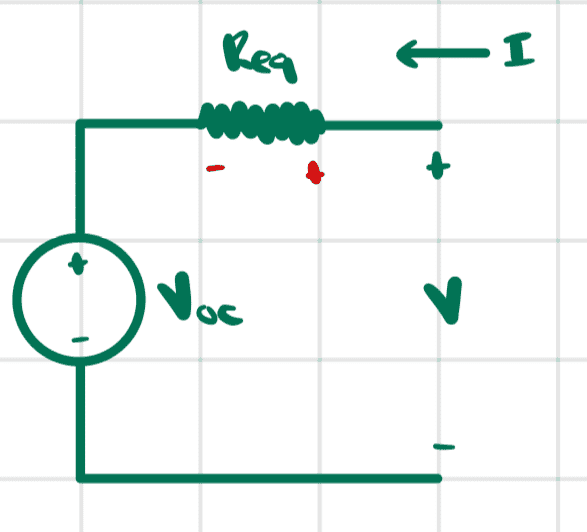
Indeed, the voltage at the terminals of this circuit is
$$V=IR_{eq}+V_{oc}=V_b+V_{oc}=\frac{R_2(\alpha+R_1)}{R_1+R_2+\alpha}(I+I_0)\tag{11}$$
One of my questions is about the second subcircuit.
How does current flow in this subcircuit?
It seems that both ##i## and ##i_2## are positive.
$$i=\frac{R_2}{R_1+R_2+\alpha}I\tag{12}$$
$$i_2=\frac{R_1+\alpha}{R_1+R_2+\alpha}I\tag{13}$$
It seems that current is flowing from positive to negative terminals of the voltage source.
In fact, we seem to have
$$e+\alpha i=\frac{R_1R_2+\alpha R_2}{R_1+R_2+\alpha}\tag{14}$$
$$e=\frac{R_1R_2}{R_1+R_2+\alpha}\tag{15}$$
Thus, ##e+\alpha i>e##.
But then current would need to flow from the ##e## node to the ##e+\alpha i## node, right?
In summary, how does current flow through the dependent voltage source in the second sub-circuit above?
I am really not confident that the attempted solution below is correct.
Let's put a test current source between the terminals we're interested in
First let's compute the open circuit voltage. We set the newly introduced test current source to zero and compute the voltage between the terminals.
We have three unknowns ##e, i,## and ##i_2##.
We have three equations
$$I_0=i+i_2\tag{1}$$
$$i_2=\frac{e+\alpha i}{R_2}\tag{2}$$
$$i=\frac{e}{R_1}\tag{3}$$
Sub (3) into (2) to obtain
$$i_2=\frac{e(R_1+\alpha R_2)}{R_1R_2}\tag{4}$$
Now sub (2) and (4) into (1) and solve for ##e## to obtain
$$e=\frac{R_1R_2I_0}{R_1+R_2+\alpha}\tag{5}$$
Then
$$i=\frac{e}{R_1}=\frac{R_2I_0}{R_1+R_2+\alpha}\tag{6}$$
The open-circuit voltage is ##e+\alpha i## and this is
$$V_{oc}=e+\alpha i=\frac{R_2(\alpha+R_1)}{R_1+R_2+\alpha}I_0\tag{7}$$
Next, we set current source ##I_0## to zero and we solve for the voltage on the terminals we're interested in.
We have the same three unknowns as before, and the equations turn out to be the same as before except that instead of ##I_0## we have ##I## in the equations.
Thus, for this subcircuit we have
$$V_b=e+\alpha i=\frac{R_2(\alpha+R_1)}{R_1+R_2+\alpha}I\tag{8}$$
The Thevenin equivalent resistance is
$$R_{eq}=\frac{R_2(\alpha+R_1)}{R_1+R_2+\alpha}\tag{9}$$
By superposition, the voltage at the terminals of the original circuit is
$$V=V_{oc}+V_b=\frac{R_2(\alpha+R_1)}{R_1+R_2+\alpha}(I+I_0)\tag{10}$$
The Thevenin equivalent circuit is
Indeed, the voltage at the terminals of this circuit is
$$V=IR_{eq}+V_{oc}=V_b+V_{oc}=\frac{R_2(\alpha+R_1)}{R_1+R_2+\alpha}(I+I_0)\tag{11}$$
One of my questions is about the second subcircuit.
How does current flow in this subcircuit?
It seems that both ##i## and ##i_2## are positive.
$$i=\frac{R_2}{R_1+R_2+\alpha}I\tag{12}$$
$$i_2=\frac{R_1+\alpha}{R_1+R_2+\alpha}I\tag{13}$$
It seems that current is flowing from positive to negative terminals of the voltage source.
In fact, we seem to have
$$e+\alpha i=\frac{R_1R_2+\alpha R_2}{R_1+R_2+\alpha}\tag{14}$$
$$e=\frac{R_1R_2}{R_1+R_2+\alpha}\tag{15}$$
Thus, ##e+\alpha i>e##.
But then current would need to flow from the ##e## node to the ##e+\alpha i## node, right?
In summary, how does current flow through the dependent voltage source in the second sub-circuit above?
Last edited: