Kaushik
- 282
- 17
- Homework Statement
- A small block ##m## is projected with speed ##v_0 = \sqrt{2gR}## from bottom of a fixed sphere of radius ##R## , so that the block moves in a vertical circular path.
- Relevant Equations
- Attached below.
Does the block move along the pink dotted lines as attached in the figure below?
I tried to draw the FBD of the small block ##m ## at the lowermost point which is also attached below.(The direction of ## v_0 ## is actually tangential)
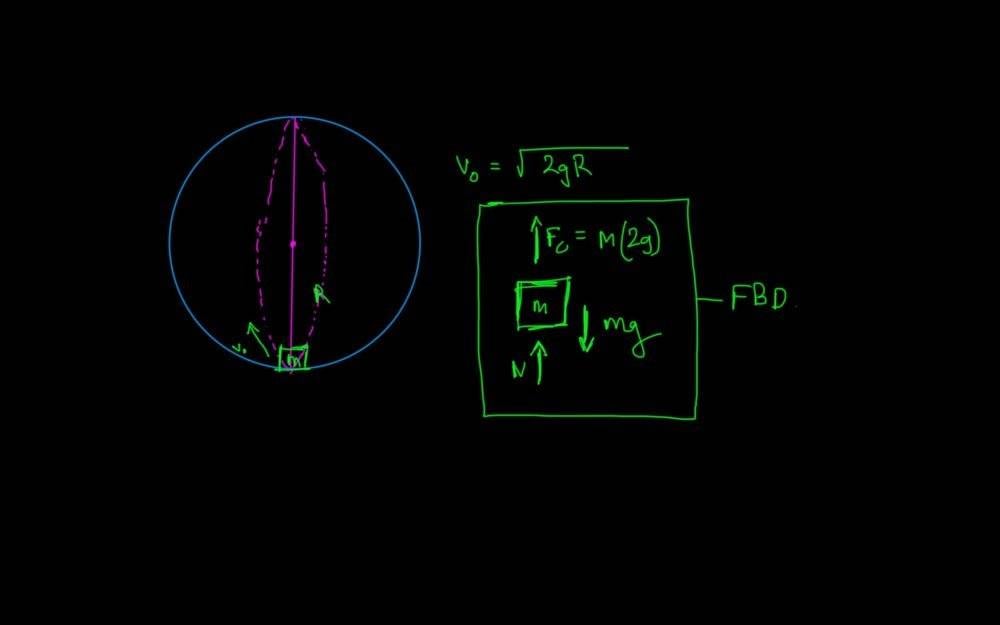
Is the figure above correct? If not, why?
I tried to draw the FBD of the small block ##m ## at the lowermost point which is also attached below.(The direction of ## v_0 ## is actually tangential)
Is the figure above correct? If not, why?