karuthamma
- 3
- 0
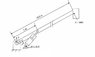
There is boom crane with a bucket attached at the end. The angle of the boom "theta" is 60 degree. The weight of the bucket with a man in it is 200Kg. The mass of the boom is acting at centre of the boom (length of the boom is 10m) is 600 Kg.
There is a cylinder attached to lift the boom 1m from the boom hinge. The hinge of the cylinder is (0.5, -0.3) with respect to the boom hinge (0,0).
Stiffness of the boom modeled by a rotational spring attached at boom hinge is 3x10^5 Nm/rad.
The Cylinder modeled as spring (K= 4x10^6 Nm)and a damper
Assume, 1degree freedom for the oscillation of the crane.
(i)Find Diff. eqn. using Newtons 2nd law of rotational motion at boom's hinge
(ii)Crane natural frequency
(iii)Derive the transfer motion for angular motion as function of wind force F (F=500N, constant & normal to the boom)
I HAVE DONE MY CAL. BUT PLEASE HELP ME IN GUIDING THE APPROACH.
There is a cylinder attached to lift the boom 1m from the boom hinge. The hinge of the cylinder is (0.5, -0.3) with respect to the boom hinge (0,0).
Stiffness of the boom modeled by a rotational spring attached at boom hinge is 3x10^5 Nm/rad.
The Cylinder modeled as spring (K= 4x10^6 Nm)and a damper
Assume, 1degree freedom for the oscillation of the crane.
(i)Find Diff. eqn. using Newtons 2nd law of rotational motion at boom's hinge
(ii)Crane natural frequency
(iii)Derive the transfer motion for angular motion as function of wind force F (F=500N, constant & normal to the boom)
I HAVE DONE MY CAL. BUT PLEASE HELP ME IN GUIDING THE APPROACH.