temaire
- 275
- 0
Homework Statement

3The attempt at a solution
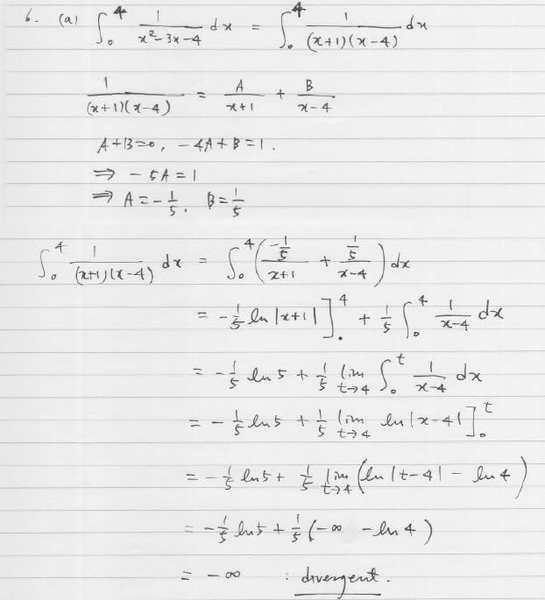
Is this correct?
3The attempt at a solution
Is this correct?
temaire said:Do I need to show that I'm approaching 4 from the right?
Dick said:I would say you are approaching 4 from the left. t<4, correct? Why would you want to approach from the right?
Dick said:The problem with your integral is at x=4. To resolve it as an improper integral you want to integrate from x=0 to x=4-epsilon where epsilon>0. That means you are approaching the upper limit from the left. You don't care what the limit is from the right.
temaire said:So even though the limit is approaching 4 from the left at ln|x-4|, we're infact evaluating the limit as it approaches 4 from the left of 1/(x^2-3x-4)?