masamune
- 15
- 0
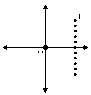
1) In the first quadrant (x > 0, y > 0), the x-component of the net electric field is:
always positive.
always negative.
sometimes positive and sometimes negative.
2) In the third quadrant (x < 0, y < 0), the x-component of the net electric field is:
always positive.
always negative.
sometimes positive and sometimes negative.
For the first part, I explained that in the first quadrant, the x and y components of the field are both positive and so the net electric electric field will always be positive. Conversely, in the third quadrant, the x and y components of the field are always negative and so the net electric field will always be negative. Is my rationale correct? Refer to the attached pic btw if you have no clue what I'm talking about.
always positive.
always negative.
sometimes positive and sometimes negative.
2) In the third quadrant (x < 0, y < 0), the x-component of the net electric field is:
always positive.
always negative.
sometimes positive and sometimes negative.
For the first part, I explained that in the first quadrant, the x and y components of the field are both positive and so the net electric electric field will always be positive. Conversely, in the third quadrant, the x and y components of the field are always negative and so the net electric field will always be negative. Is my rationale correct? Refer to the attached pic btw if you have no clue what I'm talking about.