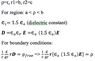- #1
tquiva
- 20
- 0
Homework Statement
I am given the following problem:
[URL]http://forum.allaboutcircuits.com/attachment.php?attachmentid=35938&d=1320027350[/URL]
Homework Equations
The Attempt at a Solution
My known equations and attempt to the problem:
[URL]http://forum.allaboutcircuits.com/attachment.php?attachmentid=35940&stc=1&d=1320028178[/URL]
Basically, my answer to the problem is not the same as the book's answer, and I'm pretty sure I'm using the right equations. What could I possibly be doing wrong here? I've been trying to figure this out for three hours now, and am now frustrated. I apologize for my ignorance here, but any advice or tips will be greatly appreciated.
Last edited by a moderator: