basenne
- 20
- 0
1. In Figure 8-49, a block is sent sliding down a frictionless ramp. Its speeds at points A and B are 1.90 m/s and 2.60 m/s, respectively. Next, it is again sent sliding down the ramp, but this time its speed at point A is 3.85 m/s. What then is its speed at point B?
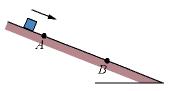
Figure 8-49
2. KE = 1/2mv^2
PE = mg (h)
3. 1/2(m)(2.2^2) + m(9.8)(h) = 1/2(m)(2.6^2) + m(9.8)(.5h)
Yes, I know now that I can't assume that the height for point b is .5 of the height for point A. I'm totally lost on this question and I'd really appreciate a push in the right direction.
Figure 8-49
2. KE = 1/2mv^2
PE = mg (h)
3. 1/2(m)(2.2^2) + m(9.8)(h) = 1/2(m)(2.6^2) + m(9.8)(.5h)
Yes, I know now that I can't assume that the height for point b is .5 of the height for point A. I'm totally lost on this question and I'd really appreciate a push in the right direction.