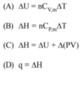cooldudeachyut
- 5
- 0
Homework Statement
Match the following
Given : Processes do not include chemical reactions. Assume CP,m and CV,m are independent of temperature for given substance and consider only pressure-volume work in given all processes.
Homework Equations
ΔU = Q - W
ΔH = ΔU + Δ(PV)
PV = nRT
The Attempt at a Solution
The answer's given as following -
A : P Q S
B : P Q R
C : P Q R S T
D : P R T
I can get all relations correct except I don't understand why A : R and B : S aren't right. Since it says "any substance" I think those options should be right even if they only work for an ideal gas.
For an isochoric process ΔV = 0, so
ΔU = Q = nCV,mΔT
ΔH = ΔU + VΔP
VΔP = nRΔT
which gives the relation as,
ΔH = n(CV,m + R)ΔT
Since CP,m - CV,m = R, I can conclude that
ΔH = nCP,mΔT
Similarly for an isobaric process ΔP = 0, so
ΔU = Q - PΔV , where Q = nCP,mΔT
PΔV = nRΔT
which gives the relation as,
ΔU = n(CP,m - R)ΔT
and just like before it becomes,
ΔU = nCV,mΔT
I also remember reading somewhere that equations in option A and B work for any process, so maybe relations A : T and B : T are correct as well but I cannot derive for them.