Equation is to get the torque on a wheel

[Jdo300]

Hello All,

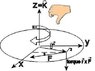
I was wondering what the equation is to get the torque on a wheel from a point (x,y) on the wheel, with an applied force vector on the point. I know I will need to use some combination of Sin or cosine, but I'm not sure how to set up the math for it. Any help would be appreciated.

Thanks,
Jason O

 

[arildno]

Use the vector cross product

 

[dextercioby]

As for sine and cosine,depends on the geometry of the problem...

Daniel.

 

[da_willem]

\vec{T}=\vec{r} \times \vec{F}
T=rFsin(\theta)

With \vec{r} the position vector from the point you want to calculate the torque \vec{T} from to the point where the force \vac{F} acts. \theta is the angle between the two. (for the definition of the cross product see eg http://mathworld.wolfram.com/CrossProduct.html)

 

[arildno]

Thank you for the equation. I checked out that link and also looked up lots of different reffereces on the cross-product. I'm guessing that since I'm getting the torque, that's the magnitude of the product vector? I was looking at this equation to compute it:

\abs(\vec{u} \times \vec{v})=\abs(\vec{u}) \abs(\vec{u}) sin(\theta)

Blasphemy!
\vec{u}\times\vec{v}=||\vec{u}||||\vec{v}||\sin\theta

 

[Jdo300]

Sorry, I was trying to write something and it came out wrong. Just a sec...

 

[Jdo300]

OK, I See the two equations \vec{T}=\vec{r} \times \vec{F} and T=rFsin(\theta) but I'm not sure how to apply them to what I want to do. Here's what I know. I know the position of the point that I'm looking at, and I know how much X and Y force is being exerted on that point. Like for example, if my point is (2,3) and there is 3 Newtons of force exerted in the negative Y direction and 1 Newton exerted on it in the positve X direction, how would I turn this into a torque measurment using these equatrions and knowing that the axis of rotation is at (0,0)? Could someone show me how to set it up using the measurments I provided?

Thanks,
Jason O

 

[arildno]

Sure; let \vec{r}=(x,y) be the point where the force acts, and \vec{F}=(F_{x},F_{y} the force in component form.
Then, the torque from \vec{F} is by definition of the cross product equal to:
\vec{r}\times\vec{F}\equiv(xF_{y}-yF_{x})\vec{k}
where \vec{k} is the normal to the xy-plane.

 

[Jdo300]

Sure; let \vec{r}=(x,y) be the point where the force acts, and \vec{F}=(F_{x},F_{y} the force in component form.
Then, the torque from \vec{F} is by definition of the cross product equal to:
\vec{r}\times\vec{F}\equiv(xF_{y}-yF_{x})\vec{k}
where \vec{k} is the normal to the xy-plane.

Ok... Let me see if I got this straight. If I use the numbers I mentioned, then would the \vec{r} would be (2,3) and would the \vec{F} would be (1,-3)? Now, after getting here: \vec{r}\times\vec{F}\equiv(xF_{y}-yF_{x})\vec{k}, that's where you completely lost me I even looked this up but I'm not sure what to do with it.

 

[dextercioby]

How about plugging in the numbers??
\vec{r}=(2,3)\Rightarrow x=2;y=3
\fec{F}=(1,-3)\Rightarrow F_{x}=1;F_{y}=-3

Daniel.

 

[Jdo300]

How about plugging in the numbers??
\vec{r}=(2,3)\Rightarrow x=2;y=3
\fec{F}=(1,-3)\Rightarrow F_{x}=1;F_{y}=-3

Daniel.

Hi, I think I sort of get the idea for the equations. My main problem is that I've never worked with vector equations before. But I'm trying to figure this out. I got stuck again but here's how I approached it with what you've given me:

\vec{r}\times\vec{F}\equiv(xF_{y}-yF_{x})\vec{k}

(2,3)\times(1,3) = (2(-3) -3(1))\vec{k}

(2,3)\times(1,3) = (-6 -3)\vec{k}

(2,3)\times(1,3) = (-9)\vec{k}

\frac{(2,3)\times(1,3)}{-9} = \vec{k} ?

I'm assuming that the value I'm solving for is the magnitude of \vec{k} but am I setting this problem up correctly?? If so, where do I go from here to get the torque value?

 

[da_willem]

...

(2,3)\times(1,3) = (-9)\vec{k}

\frac{(2,3)\times(1,3)}{-9} = \vec{k} ?

I'm assuming that the value I'm solving for is the magnitude of \vec{k} but am I setting this problem up correctly?? If so, where do I go from here to get the torque value?

Actually you already found your answer. You applied the definition: \vec{T}=\vec{r} \times \vec{F} and found an answer: (2,3)\times(1,3) = (-9)\vec{k}, now al you have to do is interpret your outcome. For this you have to realize a torque is a vector quantity, it has a magnitude (-9) and a direction \vec{k} (better would be to write the unit normal in the z-direction: \hat{k} so it is clear the magnitude of this (unit-) vector is unity)

So you have a torque of -9 Nm in the z-direction or 9 Nm in the -z-direction!

This shows you some of the properties of the cross product definition of a torque; the torque will be always perpendicular to both the radius and the force. And the magnitude is not simply the product of both but depends on the angle the two make. The latter is easy to interpret, The 'more perpendicular' the force is to the radius the larger the torque.

The direction of the torque isn't that obvious. If you have made a drawing of the situation you will ofcourse know whatis going to happen. The torque wants to move your point clockwise (as seen from the z-direction). This is indicated by your result that the torque is in the -z-direction. The rule to find the effect of a torque is called the 'righthand rule'. You put the thumb of your righthand in the direction of the torque you calculated (the -z-direction) and your fingers will indicate which direction the point will move.

 

[Jdo300]

Ahhhhh :-) Okay, I think I'm finally getting this now. Let me make sure I completely understand this now. I have -9 as the magnitude of my torque. Now, I just want to make sure that what I'm thinking is right, This value of -9 correspond to the rotational force on the wheel right? I drew up and attached a cheapo digram just to ensure that my understanding is correct. In my diagram, if the black arrow represents the vector produced by the X and Y vectors, and the blue arrow represents the amount of rotational force, -9 would go with the magnitude of that rotational force right? And with what you were saying about the right hand rule, a positive value = counterclockwise rotation and a negative value represents clockwise rotation when the Z axis is pointing toward you right?

Just want to make sure I thoroughly understand this. Ok, one more question too, about that \vec{k}, are the coordinates that represent that the (2,3)\times(1,3) that's to the left of the equal sign (before I divided it all by -9). If so, then what do you do with them to get the X, Y coordinates of the perpendicular vector?

Thank you,
Jason O

 

[da_willem]

Maybe this spicture clears things up. For an explanation of the right hand rule to find out the direction of a cross product see for example http://www.ac.wwu.edu/~vawter/PhysicsNet/Topics/MagneticField/RightHandRule.html or for more information on the cross product http://en.wikipedia.org/wiki/Cross_product

 

[Jdo300]

OK, thanks for he graphic. I'm still trying to relate that vector that is perpendiculer to the torque force. I was reading through the article you gave me the link for and I also looked at the site's article on torque. I saw one of their equations for torque which was T = (moment arm)\times Force and T = (distance to center)\times Force. Is the magnitude of the perpendicular vector equal to the magnitude of the moment arm vector used in the above torque equations (trying to reduce this to a 2D view).

 

[dextercioby]

For an explanation of the right hand rule to find out the direction of a cross product see for example [/QUOTE] How about the corkscre...e right hand rule...Figers may be lost... :-p

 

[da_willem]

OK, thanks for he graphic. I'm still trying to relate that vector that is perpendiculer to the torque force. I was reading through the article you gave me the link for and I also looked at the site's article on torque. I saw one of their equations for torque which was T = (moment arm)\times Force and T = (distance to center)\times Force. Is the magnitude of the perpendicular vector equal to the magnitude of the moment arm vector used in the above torque equations (trying to reduce this to a 2D view).

Actually this is the first thing I wrote down for you:

\vec{T}=\vec{r} \times \vec{F}
T=rFsin(\theta)

With \vec{r} the position vector from the point you want to calculate the torque \vec{T} from to the point where the force \vac{F} acts. \theta is the angle between the two. (for the definition of the cross product see eg http://mathworld.wolfram.com/CrossProduct.html)

With this all you need to know is the meaning of the 'x' called the cross product:

let \vec{r}=(x,y) be the point where the force acts, and \vec{F}=(F_{x},F_{y} ) the force in component form.
Then, the torque from \vec{F} is by definition of the cross product equal to:
\vec{r}\times\vec{F}\equiv(xF_{y}-yF_{x})\vec{k}
where \vec{k} is the normal to the xy-plane.

Among the properties of the cross product is that the resulting vector is perpendicular to both! vectors you are 'cross product-ing'. So that's why Your torque is in the direction perpendicular to the wheel (as the force and the 'arm' are both in the plane of the wheel). That about the direction of the torque

Now the magnitude: the magnitude is proportional to both vectors in the cross product. In your case the torque is proportional to both the arm and the force. It is also proportional to the sine of the angle between both:

\vec{T}=\vec{r} \times \vec{F}
T=rFsin(\theta)

The resulting magnitude is equal to the area of the paralellogram spanned by both vectors in the cross product! In your case if you draw a paralellogram by using the force and the arm as the 'arms', the area is equal to the magnitude of the cross product.

this angle dependence is ofcourse required because if you apply a force in the direction of your arm the object will be displaced, not rotated! So in that case the angle is zero or 180 degrees, the sine is zero and the torque is zero. The torque is maximum when the arm and force are perpendicular in which case the sine is unity and the torque is just rF. Also the parallelogram is just a rectangle and the area is just rF...

 

[Jdo300]

Hmmm... well, based on what you have told me, it would seem that the simplest formula to use would be T=rFsin(\theta) since in my case, I already know that the direction of the torque will be perpendicular to \vec{r} in the same plain on my wheel. Now, looking at this as far as solving it, how do I get the \theta to plug into the sine function? I know that it represents the angle between the r vector and the F vector but what trig should I use to get the angle to input into the function?

 

[Jdo300]

Ok, here's me taking a stab at this again. Would this work?

T = rFSin(ACos([r^2 + F^2 - d^2] / 2rF))

All I did was replace theta with the law of cosines using r and F as the distance part of the vectors and d as the distance between the ends of the vectors (to make a closed triangle). Am I close?

 

[da_willem]

I think it is better to use your knowledge of the forces and the arm because you don't know anything about the angles. So it is better to use: \vec{T}=\vec{r}\times\vec{F}=(xF_{y}-yF_{x})\vec{k} and for the magnitude: T=(xF_{y}-yF_{x}) as k is a unit vector and has thus a magnitude of unity. (note the difference in \vec{T} and T between a vector and it's magnitude)

 

[Jdo300]

Ahhhh! I see. I didn't know it was that simple. When I say that equation the first time, I got confused by the \vec{k} that was there and I wasn't sure how to deal with it. But thank you very much for helping me to understand it all.

 

[arildno]

Jdo:
Here's how you shouldn't be confused by \vec{k}
In your case, the object will rotate in the xy-plane (right?)
But which vector is uniquely related to a plane?
Clearly, a plane can be designated by specifying the NORMAL VECTOR to that plane?
That is, the presence of \vec{k} in the expression for the torque merely states the fact that all rotation occurs in the (xy)-plane (or a plane strictly parallell to the xy-plane).
Think about it..

 

[Jdo300]

Hi, I understand conceptually what you mean about vector K signifying that the rotation occurs in only he X,Y plane (which is what I want). As for the remainder of the explanation, It hasn't quite clicked but I'm supposed to be learning this soon in my Physics class so I'm guessing it'll all make sense eventually. Thank you very much for your help though.

I did think of one more question. I applied the equation to my data that I'm working with (it looks great), but I'm curious to know how to deal with the unit of measure for Torque. I know that the standard Metric unit is Newton-meters, and that's what I would like to use for all my measurements, and all my forces are being outputted in Newtons, but what do you do if the point of force is 3 inches from the rotor or 11 feet? Would this be accomplished by just a simple conversion factor or is there more to it?

 

[arildno]

There is nothing more to it that using a correct conversion factor.

 

[Jdo300]

Ok, nice. Well, for anyone out there who might find it useful 1 Newton Inch = 0.0254 Newton Meters