Equivalent Capacitance of a Triangular Network of Capacitors

[connor8771]

Homework Statement

There are three capacitors connected in a triangular network as shown in the picture. What is the equivalent capacitance across terminals a and c?

Relevant Equations

C=q/delta(V)

Hi, I'm struggling with this question. I feel like I don't even know where to begin. It seems to be a relatively simple calculation, but would the effective capacitance between A and C not just be 1 microFarad? Obviously that can't be the correct answer because such a simple observation wouldn't justify a question, but I can't figure out why it would be anything different. I understand how capacitance works but can't seem to even get a handle on what this question wants of me. Thanks in advance for any help.

 

[gneill]

Can you see any opportunities for combining capacitances that are in series or parallel?

 

[connor8771]

Well evidently they are connected in series, so the total capacitance of the entire network could be calculated as 1/C = 1/C1 + 1/C2 + 1/C3... but that would be for the entire network. From A to C, there is only 1 capacitor, so wouldn't it just be the capacitance of that one?

 

[gneill]

Well evidently they are connected in series, so the total capacitance of the entire network could be calculated as 1/C = 1/C1 + 1/C2 + 1/C3... but that would be for the entire network. From A to C, there is only 1 capacitor, so wouldn't it just be the capacitance of that one?

Nope. You are asked to determine the equivalent capacitance between two points in the circuit. There's more than one path starting at (a) that ends at (c). One path is the one that goes directly from (a) to (c) via the 1 μF capacitor, what's the other path?

 

[connor8771]

The other path would be A-B-C. In which case 1/C = 1/2+1/2 = 1 so C = 1 microfarad. I thought about this. It gives the same answer as the first direction, but only by chance. In a more generalized case, 1/C1 would not necessarily equal 1/C2+1/C3. So the two paths would give different values, which is where I am confused.

 

[gneill]

The other path would be A-B-C. In which case 1/C = 1/2+1/2 = 1 so C = 1 microfarad. I thought about this. It gives the same answer as the first direction, but only by chance. In a more generalized case, 1/C1 would not necessarily equal 1/C2+1/C3. So the two paths would give different values, which is where I am confused.

Yes, you've found the other path. You don't choose just one path. You must combine the effects of all paths.

You've found the equivalent capacitance of the second path to be 1 μF . What's the relationship of that capacitance to the first path?

 

[connor8771]

Oh, the first path is in parallel with the second. Guess I didn't see it that way. So if the capacitance of the first path = C1. And the capacitance of the second path is 1/C=1/C2+1/C3 = (C3+C2)/(C2*C3) so C = C2*C3/(C2+C3). Then you would add the capacitances for the two since they are in parallel so C = C1 + C2*C3/(C2+C3)? So in this case it would be 1+2*2/(2+2) = 2 microfarads?

 

[gneill]

Yup!

Try not to get confused by diagonal lines in circuits. You can always redraw a circuit in a more "conventional" rectangular form:

 

[connor8771]

Thank you, I couldn't figure that out for the life of me. You're correct, dealing with circuits drawn in odd configurations often throws me off.

 

[epenguin]

Yes, that is one of the frequent difficulties of students initially, not recognising the equivalence of circuits according to how they are drawn.

Let me say that another unnecessary difficulty is caused by thinking always formulaically rather than physically.Physically it should be rather obvious that the total charge of several different branches in parallel is the sum of the charges in each.In brief, charges add up. They are down to the number of electrons on the negative side after all.

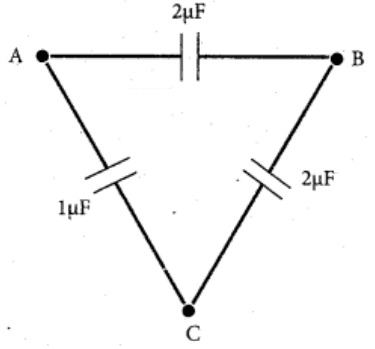
For capacitors in series bear in mind that on the internal part connected to B,
|---b--| in the diagram, there is no net charge on this part. Unlike the plates connected to A and C, there is nothing connected to supply or take away electrons. What happens is that the negative pole C, say, does supply electrons to the plate connected. Which then repel the same number of electrons from the facing internal plate onto the connected plate or, we say, induce the same number of positive charges on the facing plate. The same way the electrons on the second plate induce an equal positive charge on the plate connected to A. In other words what we loosely call the 'charge on the capacitor' is equal for the two capacitors in series, and indeed for each of any number of capacitors connected in series. Now as Q = CV, V = Q/C, and as voltages along a line add up, Q being the same for all in series it is the reciprocal capacitances that add up.

Probably better explained in any textbook, but the emphasis is so much on solving a series of problems that these basics are skipped.

Finally, students frequently miss the opportunity of using symmetry to simplify getting solutions. In your example the capacitances in branches AB and BC are equal, so voltages across each must be equal. So if e.g. V_AC = 1V, V_AB and V_BC must each be ½V, and thus the charge on each is 1μC. They don't add up! - because viewed from the outside you just have 1μC positive charge on the plate connected to A and 1μC negative charge on the plate connected to C. Could be a covenant capacitance of this series part so the equivalent capacitance of this series part is 1μC. Easier seen than explained I hope.