Figuring out Clock Desynchronization

[kratsg]

Hey, I can't seem to get my equations to work correctly to get the right numbers. I'm looking at the example here (A One Way Trip (Twin Paradox).

In the lab frame (rest frame of the planets)

I get this. Mars is separated by 100 light-seconds, and Bill travels at 0.8c. Therefore, Jim times 100/0.8 = 125 seconds. Since both Mars and Earth are synchronized in Jim's frame (simultaneous), they won't be synchronized in Bill's frame. My issue is trying to draw this picture

with the correct numbers. \beta = 0.8, \gamma = \frac{5}{3}.

t' = \gamma (t - \frac{v x}{c^2} ) \qquad\qquad x' = \gamma (x - vt)

I can see that in Bill's frame, v = -0.8c and x = 100/\gamma as the distance between the planets is Lorentz contracted. Then calculating t' for t=0 gives the 80 seconds. But I don't see the connection between what "B" represents in Jim's frame.

How do you see that "C" is along the line of simultaneity in Jim's frame?
What is "B"?
Does "B" represent when the clocks on Mars are 0 in Bill's frame of reference?
When you try to "boost" for x' - you get x' = \gamma x which isn't length contraction, what gives? Is this x' representing where the Mars planet is in Bill's frame when it was synchronized in Jim's frame?

 

[dauto]

It seems you should be setting t' = 0 instead.

 

[ghwellsjr]

I can see that in Bill's frame, v = -0.8c and x = 100/\gamma as the distance between the planets is Lorentz contracted. Then calculating t' for t=0 gives the 80 seconds. But I don't see the connection between what "B" represents in Jim's frame.

How do you see that "C" is along the line of simultaneity in Jim's frame?
What is "B"?
Does "B" represent when the clocks on Mars are 0 in Bill's frame of reference?
When you try to "boost" for x' - you get x' = \gamma x which isn't length contraction, what gives? Is this x' representing where the Mars planet is in Bill's frame when it was synchronized in Jim's frame?

It always amazes me how some authors take such a simple concept and turn it into something almost totally incomprehensible.

Here's how I process this kind of scenario. I start with the defining Inertial Reference Frame (IRF) and draw a spacetime diagram. I represent Earth (and Jim) as the blue line, Mars as the red line and Bill as the black line. The dots represent the passage of ten years for each object/observer. Since Bill is traveling at 0.8c, the spacing of his dots are dilated to 5/3 of the Coordinate Time:

You can treat each dot as an event and transform them using the Lorentz Transformation and draw them on a new diagram:

If you are doing this manually, you don't have to actually calculate the new coordinates for each dot, just do the end points of each worldline and fill in the dots proportionately. Then keep in mind that the dots are numbered with the clocks' times from bottom to top starting at zero and incrementing by ten.

Pretty simple, isn't it?

BTW, make sure you use v=0.8c (not -0.8c).

 

[kratsg]

It always amazes me how some authors take such a simple concept and turn it into something almost totally incomprehensible.

Here's how I process this kind of scenario. I start with the defining Inertial Reference Frame (IRF) and draw a spacetime diagram. I represent Earth (and Jim) as the blue line, Mars as the red line and Bill as the black line. The dots represent the passage of ten years for each object/observer. Since Bill is traveling at 0.8c, the spacing of his dots are dilated to 5/3 of the Coordinate Time

This is probably what I was looking for. It seems to me that "B" (in their diagram) is what Bill observes the clock on Mars when he is passing by Earth. Then it's clear that Bill observes the clock on Mars being ahead by 80 seconds. Then when he reaches Mars, he observes that the Mars clock reads 125 seconds - and it has only ticked 45 seconds in the time it took Bill to tick 75 seconds.

- How did you draw these? I was trying to do it in Mathematica, but that required a lot of extra coding to get all the ticks and stuff. How did you implement the transformation? (This would be a good teaching tool).

EDIT: maybe this is confusing. When Bill is passing by Earth - what does he observe the value of the clock at Mars to be? At that time, we know the value of the clock at Mars to be 80 seconds (in Bill's frame). Maybe Bill observes 50 seconds.

EDIT2:

BTW, make sure you use v=0.8c (not -0.8c).

In Bill's frame, both Mars and Earth are traveling left (the slope of the lines are 1/\beta ) where \beta = -0.8c . Which is why I used a minus sign (for direction).

 

[yuiop]

... But I don't see the connection between what "B" represents in Jim's frame.

How do you see that "C" is along the line of simultaneity in Jim's frame?
What is "B"?
Does "B" represent when the clocks on Mars are 0 in Bill's frame of reference?

I agree with ghwellsjr that the article over complicates everything. The drawing is also labelled in a confusing way. A and B are events on Earth and Mars respectively, that are simultaneous in Bill's reference frame on the outward trip. C and D are events on Earth and Mars respectively, that are simultaneous in Bill's reference frame on the return trip.

I have put some additional pairs of events on top of the original drawing in the diagram below. I hope it makes things a little clearer.

https://www.physicsforums.com/attachment.php?attachmentid=62606&stc=1&d=1381186893

The green and blue lines added to the diagram link pairs of events that are simultaneous to Bill. The event B2 (arrival at Mars and D0 (departure from Mars) are the same event relabelled and overlap in the left hand diagram.

 

[yuiop]

with the correct numbers. \beta = 0.8, \gamma = \frac{5}{3}.

t' = \gamma (t - \frac{v x}{c^2} ) \qquad\qquad x' = \gamma (x - vt)

I can see that in Bill's frame, v = -0.8c and x = 100/\gamma as the distance between the planets is Lorentz contracted. Then calculating t' for t=0 gives the 80 seconds.

When using this equation:
t' = \gamma (t - \frac{v x}{c^2} )
you are trying to find the time (t') of an event according to Bill, using t, x and v as measured by Jim. This is why you should use v = +0.8c and the time on Mars according to Bill when Bill is leaving Earth at time t=0 is -80 seconds.

When you try to "boost" for x' - you get x' = \gamma x which isn't length contraction, what gives? Is this x' representing where the Mars planet is in Bill's frame when it was synchronized in Jim's frame?

Yes, this is not length contraction. It is where Mars was at time -80 seconds according to Bill when the time according to Jim is zero on Earth and Mars. At time -80 seconds, Bill was still approaching Earth. This is not the distance between Earth and Mars as measured simultaneously by Bill. To get the length contracted distance you need to make the measurements simultaneously and then you end up with the length contraction equation. See http://hyperphysics.phy-astr.gsu.edu/hbase/relativ/tdil.html#c1

 

[ghwellsjr]

When you try to "boost" for x' - you get x' = \gamma x which isn't length contraction, what gives? Is this x' representing where the Mars planet is in Bill's frame when it was synchronized in Jim's frame?

In case you haven't figured it out yet, it is rather difficult to indicate length contraction by just plugging numbers into the Lorentz Transformation equations but if you plot the results, it becomes very clear. Look at my second diagram above. Note the distance between the blue and red lines, for example, at the Coordinate Time of 0. You will see that the location of the blue dot at t'=0 is 0 and the location of the red dot at t'=0 is 60 light-seconds. The difference between them is 60 light-seconds, the correct Length Contraction value.

By the way, this is what dauto was telling you to do.

In fact, you can do this for any value of Coordinate Time (as long as the worldlines are drawn at that time), for example, when t'=5 or t'=10.

 

[ghwellsjr]

This is probably what I was looking for. It seems to me that "B" (in their diagram) is what Bill observes the clock on Mars when he is passing by Earth. Then it's clear that Bill observes the clock on Mars being ahead by 80 seconds. Then when he reaches Mars, he observes that the Mars clock reads 125 seconds - and it has only ticked 45 seconds in the time it took Bill to tick 75 seconds.

- How did you draw these? I was trying to do it in Mathematica, but that required a lot of extra coding to get all the ticks and stuff. How did you implement the transformation? (This would be a good teaching tool).

EDIT: maybe this is confusing. When Bill is passing by Earth - what does he observe the value of the clock at Mars to be? At that time, we know the value of the clock at Mars to be 80 seconds (in Bill's frame). Maybe Bill observes 50 seconds.

I'll get to what "B" is later.

If you want to know what Bill observes as the value on the clock at Mars while he is leaving Earth, you need to start even earlier in the diagram and draw in light signals along 45-degree diagonals. These depict what is called Relativistic Doppler and show you what each observer actually sees without regard to any particular frame. In other words, you can draw the lines in on any IRF and they'll connect the source and target identically.

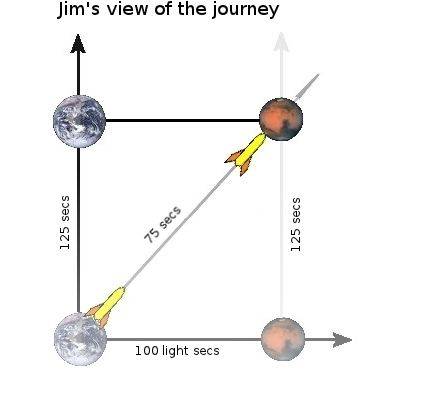
Note that at the beginning of the scenario, when Jim and Bill are colocated at the Earth, they both can look over at Mars 100 light-seconds away and see it as it appeared 100 seconds ago and they will see that the time on it is -100 seconds. Then Jim can watch Bill as he travels and every 30 seconds of Jim's time, he sees 10 seconds of Bill's time go by. He can also see 30 seconds of Mars time go by. Since the trip takes 75 seconds of Bill's time, Jim will see him arrive at Mars after 3 times 75 or 225 seconds. (I didn't draw in a signal line when this happens so you'll have to imagine it.)

Also, since Jim sees the Mars clock progressing the same as his own, but just reading 100 seconds earlier, Jim will see Bill arrive at Mars when the time of the Mars clock is reading 125 seconds.

I've also drawn in some lines propagating from Bill towards Mars. Any Martians watching this scenario will not see anything happening on Earth until they reach their time of 100 seconds. Then all of a sudden, it all happens at 3 times normal speed. So they see the 75-minute trip take only 25 seconds and ending up at 125 seconds on their clocks.

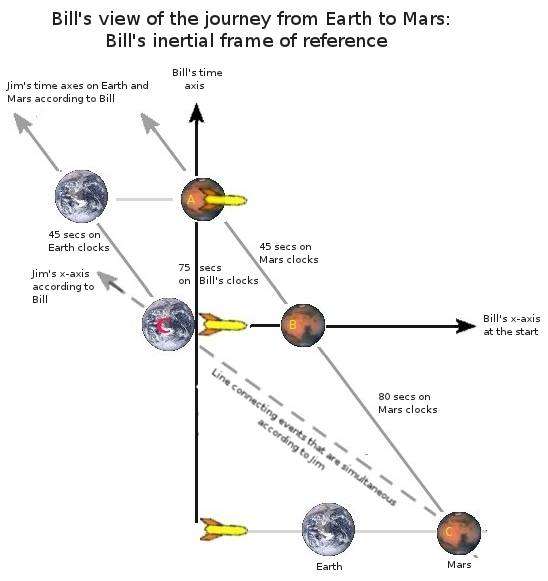
Now as far as "B" (and the other letters go) the article is adding on a return trip for Bill as shown here:

This diagram is much like the left-hand picture in the article where they discuss the whole journey. Don't worry about the letters yet.

Now we transform to Bill's rest frame during the first part of his trip:

If you look just at the region between the Coordinate Times of 0 and 75 seconds (the vertical part of the black worldline), you'll see what they are trying to depict in the bottom right-hand portion of their drawing. First you will note that they made a mistake as the arrows are pointing in the wrong direction. What they are trying to show is that the Earth starts out at the bottom, colocated with Bill and moves up diagonally to the left and ends up at position "A". Mars, on the other hand, starts out at "B" and also move up diagonally to the left and ends up above Earth's starting point. Both the Earth and Mars progress through 45 seconds during this first half of the trip. Unfortunately, the arrows imply that Earth and Mars are moving horizontally through spacetime instead of diagonally.

Now we transform to Bill's rest frame for the return part of his trip:

If you look at the region between the Coordinate Times of 345 and 420 seconds (again, the vertical part of the black worldline), you'll see what they are trying to depict in the top right-hand portion of their drawing. The Earth starts out at position "C" and progresses up and to the right and ends up above the picture of Mars. Mars starts out at the bottom and progresses up and to the right and ends up at position "D". Again, both the Earth and Mars progress through 45 seconds of their own times.

Combining the times for Earth and Mars during both portions of the trip, we get 90 seconds but we know from the first IRF that it actually takes 250 seconds so they are showing that there is a 160-second gap. This so-called gap is caused by jumping between frames. It doesn't appear in either frame by itself. Since Bill is not inertial, he cannot be depicted at rest in an IRF. However, we can construct a non-inertial frame in which he is at rest and in which light travels at c and which has no time gap. Would you be interested in seeing how that works?

EDIT2:

BTW, make sure you use v=0.8c (not -0.8c).

In Bill's frame, both Mars and Earth are traveling left (the slope of the lines are 1/\beta ) where \beta = -0.8c . Which is why I used a minus sign (for direction).

When you are converting from the original IRF shown in my first post to the second IRF, you need to use v=0.8c. If you wanted to convert the coordinates from some events in the second IRF back to the first one, you would use v=-0.8c or in the case of the return trip.

I wrote my own application to draw spacetime diagrams using a program called LabVIEW from National Instruments.

 

[ghwellsjr]

I said in the previous post that the light signals show what each observer actually sees without regard to any particular frame. To illustrate this, I'm going to show you two more transformations of Jim's rest frame depicted in the first diagram of the previous post. The first one will be transformed to a speed of 0.8c with respect to Jim's rest frame:

Note that this is Bill's rest frame.

And a second one moving at -0.8c with respect to Jim's rest frame:

Note that this isn't anybody's rest frame but it is just as valid as the other two in contrast to the erroneous claim in your article which stated:

There are only two reference frames

Here's another one, transformed to 0.5c from Jim's rest frame:

Note in this frame that everybody's clock runs at the same rate because everybody is traveling at the same speed, 0.5c. And yet, in all these IRF's, the light signals continue to convey the same information.