greg_rack
Gold Member
- 361
- 79
- Homework Statement
- FIGURE ATTACHED BELOW
##C_{1}=2.00\mu F, q_{1}=6.00\mu C, C_{2}=8.00\mu F, q_{2}=12.0\mu C##
The circuit gets closed and charge flows until the two capacitors have the same electric potential difference ##V_{F}## across its terminals.
-calculate ##V_{F}##.
- Relevant Equations
- ##q=CV##
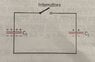
So, each capacitor must have a different potential difference, given by its capacity and charge... this would cause charge and current accordingly to flow in the circuit.
But how do I determine the final potential difference, which would of course be the same for both of them? I have tried writing down something, which I've found out to be unuseful to solve this problem.