I think I gave the right answer in #19, but anyway you are nearly there now. It is certainly unhelpful when books or teachers give wrong answers and the student is banging his head trying to find the wrong answer! It is not the only example of that I have come across here recently.
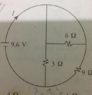
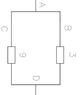
I don’t know whether this is the only reason, anyway this calculation is taking far too long! I think we have got that the 6Ω resistor has no potential difference across it, there is no current in it, it might as well not be there. So all you have we have is a single voltage source and two resistors in parallel. But that is still being found, and is often found by students, unnecessarily difficult. Let me just give my take and tips on why is simple resistive (and capacitive) steady current circuits are found more difficult than they need be.
They are found unnecessarily difficult, in my guess, because students are taught something about reciprocal resistances being the sum of other reciprocal resistances or something, which sounds arcane, mathematical, and calculational, distanced from the simple physics. Which is that current comes out of one pole of the source, divides into streams, which then reunite and the same current returns to the other pole of the source.The sum of the currents in the different streams add up to the total current at the sources. (In the context, an almost self evident principle dignified by the name Kirchoff’s Current Law or or Conservation of Charge.)
You can just calculate each of the two currents in this problem separately. Then add them together for the total current.
Didacts have maybe tried to make this simpler by a formula, but I’d say experience shows they have made it more difficult for students.
When you have got used to adding up currents in parallel parts, which won’t take long, you may realize that parallel branches with the same potential difference across them are acting like a single conductor where the ability to conduct a current – the conductance - is the sum of the conductance in each branch. Conductance, G, of a conductor is defined as
I = GV
(You can call this a definition. Many people would call that equation Ohm’s Law. Really what Ohm’s law - a generalisation from experimental findings - says is that for conductors made of many materials, and over a wide range of conditions, G is a constant.)
Then the way currents in parallel add up mean that conductances in parallel add up. I.e. several conductors G1, G2,... with the same potential difference across them conduct in total just as much as a single conductor G, with effective conductance (aka ‘ equivalent conductance‘)
G = G1 + G2 +...
which hopefully has a self-evident quality about it.
Obviously from the equation above, conductance G is the reciprocal of resistance R. I guess dicacts have tried to not overburden students with too many terms and more or less eliminate ‘conductance’ from their terminology, but the term is suggestive so I think they have lost more than they gained.
When resistors are in series on the other hand, it is potential differences that add up, and the resistance concept is more useful as the total resistance of a series of resistors is the sum of resistances.
My other tips for student circuit analysis:
Have an eye for and use any symmetry in a circuit to simplify calculation. (I only got involved in homework help for circuits because I was seeing students making unnecessarily complicated calculations which could be simplified by symmetry.)
Use rational numbers like 5⅓ in preference to decimals. Using decimals will often be wiping out information. And decimals are boring. Rationals bear a trace of the original circuit problem. (These are my reasons - I won’t make exaggerated claims for accuracy. Just once in 250 times when making accurate calculation on complicated circuit you might gain an accuracy in the third significant figure by using rationals, and of course the input data is generally not that accurate, it’s just a point of principle.) Decimals are good only for the final answer, because measuring devices use decimals.

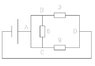

 you can conclude that teacher isn't the only one in error
you can conclude that teacher isn't the only one in error 
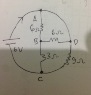
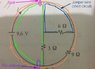
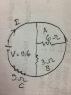
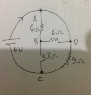
 How do I manage to get this arithmetic wrong?! Yes we could just say the current through the 3 Ω resistor is ##\frac{9.6}{3}## = 3.2 A, and then the flow through the 9 Ω resistor is a third as much = (1 + 0.2/3) adding up to (4.2 + 0.2/3) = 4.26666... ≈ 4.27 A as you say.
How do I manage to get this arithmetic wrong?! Yes we could just say the current through the 3 Ω resistor is ##\frac{9.6}{3}## = 3.2 A, and then the flow through the 9 Ω resistor is a third as much = (1 + 0.2/3) adding up to (4.2 + 0.2/3) = 4.26666... ≈ 4.27 A as you say.