Patdon10
- 85
- 0
Homework Statement
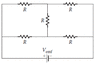
Find the equivalent resistance for the circuit in the figure. (Use the following as necessary: Vemf, R.)
Homework Equations
V=IR
The Attempt at a Solution
This problem isn't that hard, but I'm having trouble trying to visualize how to combine the resistors. The 2 most left Resistors are in parallel, as are the 2 most right ones. Those 4 are all in series with the middle resistor. How can you split it? I can't visualize it. Can anyone give me a hint?