nemisisnik
- 3
- 0
Problem:
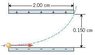
The drawing shows an electron entering the lower left side of a parallel plate capacitor and exiting at the upper right side. The initial speed of the electron is 9.42 x 10^6 m/s. The capacitor is 2.00 cm long, and its plates are separated by 0.150 cm. Assume that the electric field between the plates is uniform everywhere and find its magnitude.
What i did:
x=.5(Vo + V)t
.02m=.5(9.42 x 10^6 m/s + 9.42 x 10^6 m/s)t
solve for t=2 x 10^-9
then:
x=Vot + .5at^2
.0015m=0 + .5(a)(2 x 10^-9)^2
solve for a=8.87 x 10^15
then:
F=ma
F=(9.11 x 10^-31)(8.87 x 10^15)
F=8.08 x 10^-15
then:
E=F/q
E=8.08 x 10^-15/(1.6 x 10^-19)
E=50524.3 N/C
But that is the wrong answer, i was just wondering what i did wrong and how to correct myself.
In Addition i was wondering how to do this one?:
A long, thin rod (length = 3.0 m) lies along the x axis, with its midpoint at the origin. In a vacuum, a +7.0 C point charge is fixed to one end of the rod, and a -7.0 C point charge is fixed to the other end. Everywhere in the x, y plane there is a constant external electric field (magnitude 2.0 x 103 N/C) that is perpendicular to the rod. With respect to the z axis, find the magnitude of the net torque applied to the rod.
Thank you in advanced!
The drawing shows an electron entering the lower left side of a parallel plate capacitor and exiting at the upper right side. The initial speed of the electron is 9.42 x 10^6 m/s. The capacitor is 2.00 cm long, and its plates are separated by 0.150 cm. Assume that the electric field between the plates is uniform everywhere and find its magnitude.
What i did:
x=.5(Vo + V)t
.02m=.5(9.42 x 10^6 m/s + 9.42 x 10^6 m/s)t
solve for t=2 x 10^-9
then:
x=Vot + .5at^2
.0015m=0 + .5(a)(2 x 10^-9)^2
solve for a=8.87 x 10^15
then:
F=ma
F=(9.11 x 10^-31)(8.87 x 10^15)
F=8.08 x 10^-15
then:
E=F/q
E=8.08 x 10^-15/(1.6 x 10^-19)
E=50524.3 N/C
But that is the wrong answer, i was just wondering what i did wrong and how to correct myself.
In Addition i was wondering how to do this one?:
A long, thin rod (length = 3.0 m) lies along the x axis, with its midpoint at the origin. In a vacuum, a +7.0 C point charge is fixed to one end of the rod, and a -7.0 C point charge is fixed to the other end. Everywhere in the x, y plane there is a constant external electric field (magnitude 2.0 x 103 N/C) that is perpendicular to the rod. With respect to the z axis, find the magnitude of the net torque applied to the rod.
Thank you in advanced!