- #1
PeachBanana
- 191
- 0
Homework Statement
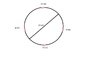
Two +4 mC charges and two -4mC charges are arranged on a circle of diameter "d" as shown in the figure below. The magnitude and direction of the force on the +4mC charge at the top of the circle is:
a) 6.39*10^6 N radially inward
b) 1.2 * 10^7 N radially inward
c) 2.4 * 10^7 N radially inward
d) 6.39 *10^6 N radially outward
e) 2.4 * 10^7 radially outward
Homework Equations
F = k q1q2 / r^2
The Attempt at a Solution
15 cm = .15 m
4 mC = 4*10^-3 C
F2,1 = (8.99*10^9 Nm^2/C^2)(-4*10^-3 C)(4*10^3 C) / (0.075 m^2)
F2,1 = -2.557*10^7 N (2) = -5.114*10^7 N
I multiplied by "2" because there are two -4mC charges.
F3,1 = (8.99*10^9 Nm^2/C^2)(-4*10^-3C)(4*10^-3C) / (0.15 m)^2
F3,1 = 6.392*10^6 N
-5.114 * 10^7 N + 6.392*10^6 N = -4.4748 * 10^7 N
Attachments
Last edited: