Dilemma
- 15
- 1
Hello everyone,
1. Homework Statement
Question : Find the volume of the region which remains inside the cyclinder x 2 + y 2 = 2y, and is bounded from above by the paraboloid surface x 2 + y 2 + z = 1 and from below by the plane z = 0
This looks like a pretty straightforward question. First thing to do is converting equations to polar coordinates. When they are converted, the cylinder's region can be written as r = 2sinθ. Parabolaid surface's eq. is (1-r2).Through these, a double integral can easily be set up as the following:
∫(from 0 to π)∫from 0 to 2sinθ) (1-r2)rdrdθ.
However, the solution to this problem proposes a different approach which does not return the same answer.
Here it is:
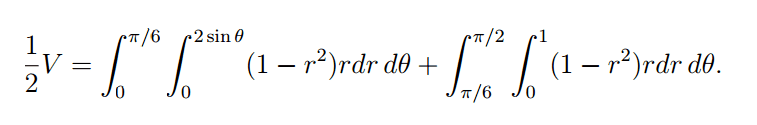
Thanks in advance,
1. Homework Statement
Question : Find the volume of the region which remains inside the cyclinder x 2 + y 2 = 2y, and is bounded from above by the paraboloid surface x 2 + y 2 + z = 1 and from below by the plane z = 0
Homework Equations
The Attempt at a Solution
This looks like a pretty straightforward question. First thing to do is converting equations to polar coordinates. When they are converted, the cylinder's region can be written as r = 2sinθ. Parabolaid surface's eq. is (1-r2).Through these, a double integral can easily be set up as the following:
∫(from 0 to π)∫from 0 to 2sinθ) (1-r2)rdrdθ.
However, the solution to this problem proposes a different approach which does not return the same answer.
Here it is:
Thanks in advance,
Last edited: