TheBigDig
- 65
- 2
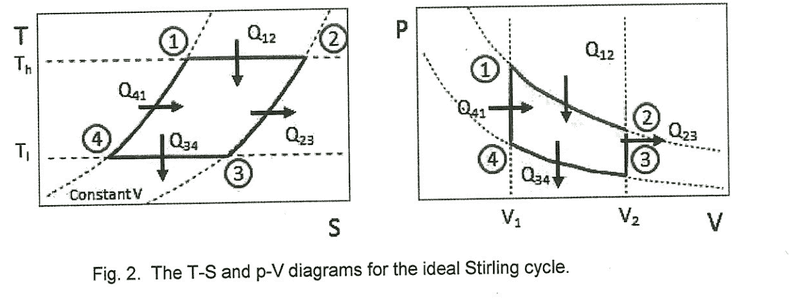
1. Given the following p-V diagram of an ideal Stirling Cycle, determine the theoretical values of W12, Q12, W34 and Q34 in terms of T1, T2, V1, V2, n (the number of moles) and R (the universal gas constant). Determine the total theoretical p-V work W12341 for the full cycle.2. dU = dQ-Pdv3. I've only just started thermodynamics recently, so my grasp on it is still very weak. I've tried finding W12 using W = -∫pdV but I'm not really sure how that gives me theoretical work. I think I'm supposed to end up with some sort of numerical answer for the final part to compare it with an actual p-V work value and find the efficiency of the Stirling Engine.