Instinctlol
- 79
- 0
QUESTION: Compute the flux of the vector field, F , through the surface, S.
F = xi+yj+zk
S is the part of the surface z = x^2 + y^2 above the disc x^2 + y^2 ≤ 4 , oriented downward.
I am just wondering why the integrand is from o to 4 while the radius is only 2.
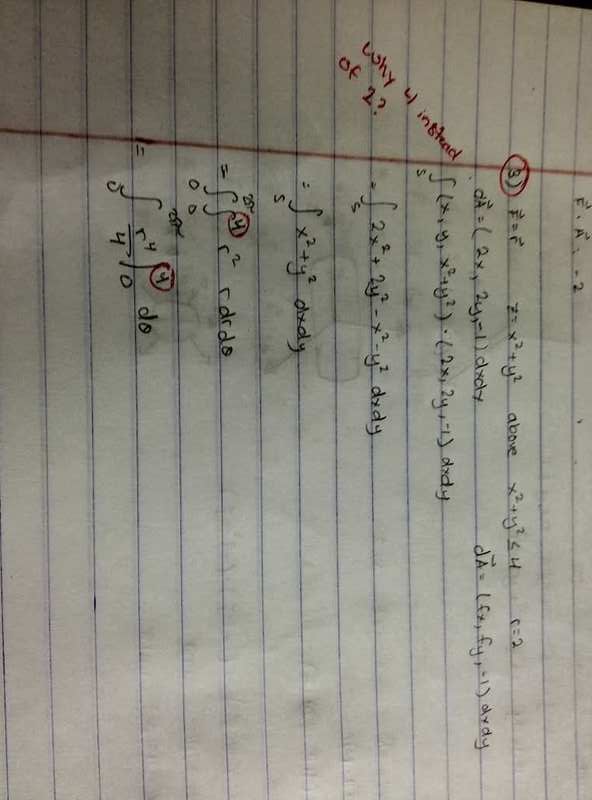
F = xi+yj+zk
S is the part of the surface z = x^2 + y^2 above the disc x^2 + y^2 ≤ 4 , oriented downward.
I am just wondering why the integrand is from o to 4 while the radius is only 2.