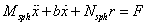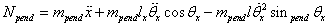SUMMARY
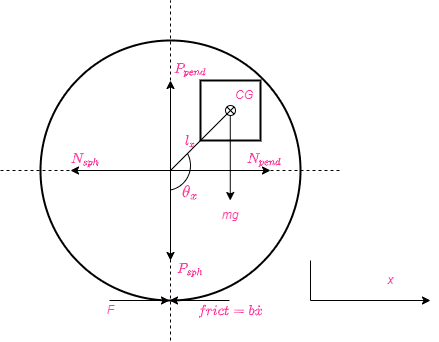
The discussion centers on the dynamics of an inverted pendulum attached to a motor shaft within a spherical enclosure, aiming to derive motion equations based on a free-body diagram. Key variables include the mass of the pendulum (mpend), mass of the spherical enclosure (Msph), and the inclination of the pendulum (theta). The motor's role is to maintain the pendulum's vertical position, necessitating a control theory approach to manage perturbations. The friction force is identified as rolling friction rather than linear friction, clarifying the mechanics involved in the system's movement.
PREREQUISITES
- Understanding of inverted pendulum dynamics
- Familiarity with control theory principles
- Knowledge of free-body diagram construction
- Basic concepts of friction types, specifically rolling friction
NEXT STEPS
- Study control theory for dynamic systems, focusing on gain factors and damping
- Learn about free-body diagram analysis in mechanical systems
- Research rolling friction mechanics and its implications in motion equations
- Explore simulation tools for modeling inverted pendulum systems
USEFUL FOR
Mechanical engineers, robotics researchers, and students studying dynamics and control systems will benefit from this discussion, particularly those interested in the application of control theory to pendulum systems.