Cinnamon
- 3
- 0
Homework Statement
A large box containing your new computer sits on the bed of your pickup truck. You are stopped at a red light. The light turns green and you stomp on the gas and the truck accelerates. To your horror, the box starts to slide toward the back of the truck. (Assume that the truck is accelerating to the right.)
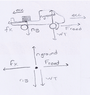
Draw clearly labeled free-body diagram for the truck. (The bed of the truck is not frictionless.)
Draw the force vectors with their tails at the dot. The orientation of your vectors will be graded. The exact length of your vectors will not be graded but the relative length of one to the other will be graded.
Homework Equations
Nground: Normal force
Nb: Reaction to the normal force on the box from the truck
Froad: Reaction force to tires' backward push
Fk: The box's friction force on the truck bed
WT: Weight of the truck
The Attempt at a Solution
Nground points up.
WT and Nb point down.
Froad points right.
Fk points left.
I made the length of Fk shorter than Froad.
I made the length of Nground = length of WT = length of Nb.
Now I'm thinking that the length of WT and Nb should be equal but together add up to the length of Nground so that the net force in the y direction is 0.