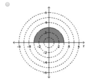
Graphing Polar Coordinates: 0 ≤ θ ≤ π and 0 ≤ r ≤ 4

Fatima Hasan
Messages
315
Reaction score
14

Homework Statement


Graph the set of points whose polar coordinates satisfy the given equation or inequality.

0 ≤ θ ≤
f1q8g1.jpg
, 0 ≤ r ≤ 4

Homework Equations


-

The Attempt at a Solution


image.png

Is it correct ?
 

Attachments

  • f1q8g1.jpg
    f1q8g1.jpg
    536 bytes · Views: 749
  • image.png
    image.png
    7.8 KB · Views: 661
Physics news on Phys.org

Homework Statement



Graph the set of points whose polar coordinates satisfy the given equation or inequality.
0 ≤ θ ≤ π, r ≤ 3

Homework Equations


-

The Attempt at a Solution


image.png

Could someone check my answer ?
 

Attachments

  • image.png
    image.png
    7.8 KB · Views: 634
Both correct.
I merged the two threads as the questions are so similar.
 
  • Like
Likes Fatima Hasan

Thread 'Prove that the integral is equal to ##\pi^2/8##'

Prove $$\int\limits_0^{\sqrt2/4}\frac{1}{\sqrt{x-x^2}}\arcsin\sqrt{\frac{(x-1)\left(x-1+x\sqrt{9-16x}\right)}{1-2x}} \, \mathrm dx = \frac{\pi^2}{8}.$$ Let $$I = \int\limits_0^{\sqrt 2 / 4}\frac{1}{\sqrt{x-x^2}}\arcsin\sqrt{\frac{(x-1)\left(x-1+x\sqrt{9-16x}\right)}{1-2x}} \, \mathrm dx. \tag{1}$$ The representation integral of ##\arcsin## is $$\arcsin u = \int\limits_{0}^{1} \frac{\mathrm dt}{\sqrt{1-t^2}}, \qquad 0 \leqslant u \leqslant 1.$$ Plugging identity above into ##(1)## with ##u...
View full post »

Similar threads

Show proof of point C in the given problem that involves Polar equation
Replies
3
Views
1K
Change of Variables: Integrals w/Polar Coordinates
Replies
2
Views
1K
Converting a Cartesian Integral to a Polar Integral
Replies
3
Views
3K
Finding the equation of a tangent line in polar coordinates?
Replies
1
Views
4K
Problem with a double integral
Replies
4
Views
1K
Double Integral in polar coordinates
Replies
12
Views
2K
Double Integration in Polar Coordinates
Replies
3
Views
2K
Evaluating Cartesian integral in polar coordinates
Replies
11
Views
2K
Trying to find this double integral using polar coordinates
Replies
14
Views
3K
Integration of acceleration in polar coordinates
Replies
24
Views
3K

Hot Threads

Recent Insights

Back
Top