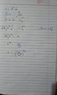Having a problem in steps while solving integrals

[prakhargupta3301]

Homework Statement

The problem is attached. I'm new to these problems (calculus).
I'm not getting my answer as any of the options. I need your help to know whether me or the slide is wrong.

Homework Equations

x_x[/B]

The Attempt at a Solution

Thank you for reading.

 

[haruspex]

What is ∫v.dv?

 

[Dr Dr news]

The slide is wrong in that x is not constant, k is constant. Your formulation is correct up to ∫ v dv as pointed out by haruspex.

 

[prakhargupta3301]

What is ∫v.dv?

It is an equation to solve kinematic equations.
a=dv/dt 1
v=dx/dt 2
Divide 1 by 2
a/v= dv/dt⋅dt/dx
a/v=dv/dx
a⋅dx=v⋅dv
Integrate LHS and RHS and you get 3rd equation of motion:
₀^x∫a⋅dx=_u^v∫v⋅dv
a⋅x₀^x=v²|_u^v
ax-0=v²/2-u²/2
2ax=v²-u²

 

[prakhargupta3301]

The slide is wrong in that x is not constant, k is constant. Your formulation is correct up to ∫ v dv as pointed out by haruspex.

So, am I correct or not ? This was quite an ambiguous reply..
If not, can you point out the mistake clearly and correction. Please?

 

[Dr Dr news]

Your LHS (2/3) k^2 x^(3/2) is OK the RHS as you have corrected is v^2 / 2 with an upper limit of 2u and a lower limit of u.

 

[haruspex]

=_u^v∫v⋅dv...=v²|_u^v

Quite so, but that does not seem to be what you wrote in your attachment in post #1. I do not see a ² there.

 

[prakhargupta3301]

Your LHS (2/3) k^2 x^(3/2) is OK the RHS as you have corrected is v^2 / 2 with an upper limit of 2u and a lower limit of u.

Quite so, but that does not seem to be what you wrote in your attachment in post #1. I do not see a ² there.

So, I was incorrect in believing v to be a constant! Silly me. (I pondered over this single question for an hour and didn't get any sleep last night xD)
Thank you both for helping me. Have a great day/night.