Eisen
- 14
- 0
Here's the circuit-
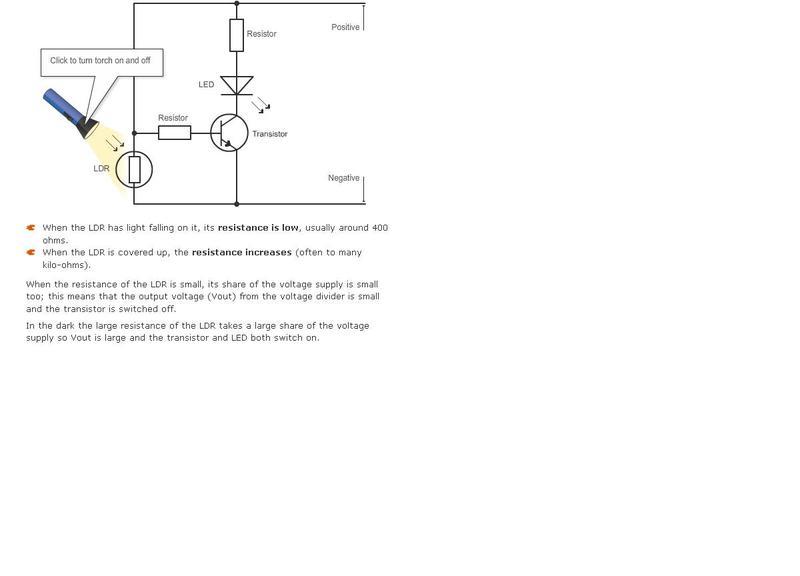
It isn't clear to me which part of this circuit makes the voltage divider and also it doesn't show where the voltage output is on the circuit. Can someone tell me those two things please. Also I don't understand why voltage increases as resistance increases in the LDR and why voltage decreases as resistance decreases in the LDR. Can someone explain that too please. It doesn't give an explanation why on this webpage I'm looking at.
It isn't clear to me which part of this circuit makes the voltage divider and also it doesn't show where the voltage output is on the circuit. Can someone tell me those two things please. Also I don't understand why voltage increases as resistance increases in the LDR and why voltage decreases as resistance decreases in the LDR. Can someone explain that too please. It doesn't give an explanation why on this webpage I'm looking at.