badman
- 57
- 0
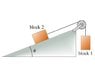
Consider another special case in which the inclined plane is vertical (\theta=\pi/2). In this case, for what value of m_1 would the acceleration of the two blocks be equal to zero?
Express your answer in terms of some or all of the variables m_2 and g.
a good point in the direction will help
Express your answer in terms of some or all of the variables m_2 and g.
a good point in the direction will help