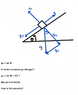
- #1
Ameer Bux
- 19
- 0
Homework Statement
The coefficient of static and kinetic friction is constant for a specific surface. On an incline plane s and k are both equal to tan of the inclined angle. If the angle increases then tan changes which means the coefficient of friction changes. How is this so?
Homework Equations
Fs = s x Fn
s = tan
The Attempt at a Solution
Attached picture