How Do You Calculate the Time Period in a Spring-Block SHM System?

[Saitama]

Homework Statement

Find the time period of the mass m as shown in the spring-block system. Neglect air resistance and pulley and springs are massless. All the three springs shown have spring constant k .

Homework Equations

The Attempt at a Solution

I am not really sure how to start with this. If the block is displaced by x, the springs $S_1$ and $S_2$ also elongate by x. But how do I calculate the displacement of $S_0$? I don't know if finding out the displacements is the correct approach.

Any help is appreciated. Thanks!

 

[Enigman]

If the block is displaced by x, the springs S1 and S2 are also elongate by x.

-How? You are getting a total displacement of 2x if both of them elongate by x.

 

[Saitama]

If the block is displaced by x, the springs S1 and S2 are also elongate by x.

-How? You are getting a total displacement of 2x if both of them elongate by x.

Does that mean they elongate by x/2? I am still not sure what to do.

 

[Enigman]

Life would be so much simpler without just one spring...

 

[Saitama]

Life would be so much simpler without just one spring...

Are you hinting at finding the equivalent spring constant?

 

[Enigman]

Warning proceed at your own risk, I'm not completely sure if I'm correct- let's say 89%
The S1 and S2 can be considered as a serial combination. Find S.H.M eq of that. Then calculate the force on the pulley, find displacement of S3, Find Shm eq of pulley, add the two eq up- get time period.
Tell me if it works, too lazy to work it out myself.

 

[Saitama]

Warning proceed at your own risk, I'm not completely sure if I'm correct- let's say 89%
The S1 and S2 can be considered as a serial combination. Find S.H.M eq of that. Then calculate the force on the pulley, find displacement of S3, Find Shm eq of pulley, add the two eq up- get time period.
Tell me if it works, too lazy to work it out myself.

The series combination is equivalent to k/2. If the block is displaced by x, the force in the string connected with $S_0$ is kx. Now how do I find the equivalent, I have a pulley in the set-up.

 

[Enigman]

Simple- don't, add both displacement-time equations of the two shm and use some trigo.
BTW what about gravity?

 

[Chestermiller]

Let the downward displacement of the lower end of spring 3 = δ₃
Let the upward displacement of the upper end of spring 2 = δ₂
Let the downward displacement of the upper end of spring 1 = δ₁
Let the downward displacement of the mass m = δ_m
Kinematically, how is δ₁ related to δ₂ and δ₃? How is the increased tension (relative to equilibrium) in spring 3, T₃, related to δ₃? How is the increased tension (relative to equilibrium) in spring 2, T₂, related to δ₂? How is the increased tension (relative to equilibrium) in spring 1, T₁, related to δ₁ and δ_m? How is the tension in spring 2 related to the tension in spring 1?

Chet

 

[Saitama]

Let the downward displacement of the lower end of spring 3 = δ₃
Let the upward displacement of the upper end of spring 2 = δ₂
Let the downward displacement of the upper end of spring 1 = δ₁
Let the downward displacement of the mass m = δ_m
Kinematically, how is δ₁ related to δ₂ and δ₃?

$\delta_3=2\delta _1=2\delta _2$?

How is the increased tension (relative to equilibrium) in spring 3, T₃, related to δ₃? How is the increased tension (relative to equilibrium) in spring 2, T₂, related to δ₂? How is the increased tension (relative to equilibrium) in spring 1, T₁, related to δ₁ and δ_m? How is the tension in spring 2 related to the tension in spring 1?

Is it wrong to say $\delta_m=\delta_1$?

 

[Chestermiller]

$\delta_3=2\delta _1=2\delta _2$?

Not really. If the pulley did not move (δ₃=0), then δ₁ would be equal to δ₂. If the pulley moved down, but spring 2 did not stretch (δ₂=0), δ₁ would be equal to δ₃. But, if the pulley moves down and spring 2 stretches, then δ₁=δ₂+δ₃.

Is it wrong to say $\delta_m=\delta_1$?

If spring 1 stretches, then δ_m does not equal δ₁.

Chet

 

[Saitama]

If spring 1 stretches, then δ_m does not equal δ₁.

Sorry but I still don't get it. :(

For example, consider a spring attached to the ceiling and a mass is hanging at the end of spring. If mass descends by $\delta_m$, then the spring also stretches by $\delta_m$, why doesn't the same apply here?

 

[Chestermiller]

Sorry but I still don't get it. :(

For example, consider a spring attached to the ceiling and a mass is hanging at the end of spring. If mass descends by $\delta_m$, then the spring also stretches by $\delta_m$, why doesn't the same apply here?

The upper end of spring 1 is not attached to the ceiling (or any other rigid constraint). It is free to move up and down. And it does move up and down. The amount that spring 1 stretches is amount that the bottom end moves downward minus the amount that the upper end moves downward.

 

[ehild]

The springs can stretch independently. The length connecting S1 and S2 stays constant. How does the change of length of an individual spring related to the displacement of the mass? Look at the figure. If the upper spring S3 stretches by δ, the pulley moves downward, the piece of string connected to S2 gets shorter by δ, so the right piece has to get longer by δ. What is the resulting displacement of the block?
If S2 stretches only, the left piece of the string gets shorter, the right piece gets longer. What about the block?
It is easy with S1.

ehild

 

[Chestermiller]

Sorry but I still don't get it. :(

For example, consider a spring attached to the ceiling and a mass is hanging at the end of spring. If mass descends by $\delta_m$, then the spring also stretches by $\delta_m$, why doesn't the same apply here?

The amount that spring 1 stretches is equal to the downward displacement of its lower end (δ_m) minus the downward displacement of its upper end (δ₁). Note that both ends of this spring can move.

 

[Saitama]

Look at the figure. If the upper spring S3 stretches by δ, the pulley moves downward, the piece of string connected to S2 gets shorter by δ, so the right piece has to get longer by δ. What is the resulting displacement of the block?

2δ?

I still have trouble understanding it. For instance, if there were no S1 and S2, the displacement of block would have been 2δ. Correct?

 

[ehild]

Yes, if neither S1 nor S2 changed length, the displacement of the block would be 2δ.

ehild

 

[Saitama]

Yes, if neither S1 nor S2 changed length, the displacement of the block would be 2δ.

ehild

Well..now what should I do?

 

[ehild]

How do you get the displacement of the block if all springs stretch, by δ1, δ2, δ3?

 

[Chestermiller]

Well..now what should I do?

To expand on what echild wrote in response #17, I suggest you follow the set of steps I outlined in response #9. In response #11, I indicated that δ₁ would be related to δ₂ and δ₃ by:
δ₁=δ₂+δ₃
But, in subsequent postings, echild showed this result to be incorrect, and that the correct relationship should be
δ₁=δ₂+2δ₃
The amount that spring 3 stretches is δ₃. The amount that spring 2 stretches is δ₂. The amount that spring 1 stretches is δ_m-δ₁. Follow the rest of the steps in my response #9 to get the tensions and to do the force balances on the pulley and on the mass.

Chet

 

[Saitama]

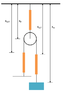
To expand on what echild wrote in response #17, I suggest you follow the set of steps I outlined in response #9. In response #11, I indicated that δ₁ would be related to δ₂ and δ₃ by:
δ₁=δ₂+δ₃
But, in subsequent postings, echild showed this result to be incorrect, and that the correct relationship should be
δ₁=δ₂+2δ₃
The amount that spring 3 stretches is δ₃. The amount that spring 2 stretches is δ₂. The amount that spring 1 stretches is δ_m-δ₁. Follow the rest of the steps in my response #9 to get the tensions and to do the force balances on the pulley and on the mass.

Honestly, I cannot see how you both easily reach the conclusion that δ₁=δ₂+2δ₃. But I have tried something else. Please review it.

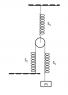
In the attachment, I have marked the distances from the ceiling. $x_{S1T}$ is the distance of top end of S1 from the ceiling. Similarly, $x_{S2T}$ is defined. I haven't marked two distances i.e the distances of bottom ends of S1 and S2 because there was not enough space. I call them $x_{S1D}$ and $x_{S2D}$ respectively.

I now use the fact that length between S1 and S2 and between S1 and m stays constant. Let $l_1$ be the length of spring between S1 and S2.
$$l_{1i}=x_{S1T}-x_P+x_{S2T}-x_P$$
When the three spring stretches,
$$l_{1f}=x_{S2T}-\delta_2-(x_P+\delta_3)+x_{S1T}'-(x_P+\delta_3)$$
where $x_{S1T}'$ is the distance of top end of S1 when the spring stretches.
$\because l_{1f}-l_{1i}=0$
$$x_{S1T}'-x_{S1T}=\delta_2+2\delta_3$$

Similarly, I apply this constraint for the string between S1 and m. Let the length be $l_2$.
$$l_{2i}=x_m-x_{S1D}$$
$$l_{2f}=x_m+\delta_m-x_{S1D}'$$
Again, $l_{2f}-l_{2i}=0 \Rightarrow x_{S1D}'-x_{S1D}=\delta_m$
The change in length of spring S1 is $\delta_1$, hence
$$x_{S1D}'-x_{S1T}'-(x_{S1D}-x_{S1T})=\delta_1$$
$$\Rightarrow \delta_m=\delta_1+\delta_2+2\delta_3$$

Okay, this gives me a relation between elongation of springs and the displacement of block but I still don't end up with the relation you both have posted. :(

 

[ehild]

$$\Rightarrow \delta_m=\delta_1+\delta_2+2\delta_3$$

Okay, this gives me a relation between elongation of springs and the displacement of block but I still don't end up with the relation you both have posted. :(

I haven't posted any relation for δm. Your equation is just what I have suggested by my picture. If S3 stretches by δ3 the mass goes down by 2δ3. If S2 stretches by δ2 the mass moves down by δ2. If S1 stretches by δ1 the mass goes down by δ1. The effect of all springs to the displacement of the mass is $$\delta_m=\delta_1+\delta_2+2\delta_3$$

Make the free-body diagrams both for the mass and the pulley. As the pulley is massless, T1=T2. Use Hook's law for the tensions, T=kδ for all springs.

ehild

 

[Saitama]

I haven't posted any relation for δm. Your equation is just what I have suggested by my picture. If S3 stretches by δ3 the mass goes down by 2δ3. If S2 stretches by δ2 the mass moves down by δ2. If S1 stretches by δ1 the mass goes down by δ1. The effect of all springs to the displacement of the mass is $$\delta_m=\delta_1+\delta_2+2\delta_3$$

That's a very nice and neat way to explain it. It is much easier instead of making the constraint equations. Thank you.

Make the free-body diagrams both for the mass and the pulley. As the pulley is massless, T1=T2. Use Hook's law for the tensions, T=kδ for all springs.

From T1=T2, $\delta_1=\delta_2$. Also, T3=T1+T2, $\Rightarrow \delta_3=2\delta_1$.
Hence, $\delta_m=6\delta_1$. The restoring force acting on m is due to spring i.e T1 and its magnitude is $k\delta_1=k\delta_m/6$.

Therefore, the time period is $$2\pi\sqrt{\frac{6m}{k}}$$. Looks correct?

Thanks a lot ehild and Chet! :)

 

[Chestermiller]

That's a very nice and neat way to explain it. It is much easier instead of making the constraint equations. Thank you.

From T1=T2, $\delta_1=\delta_2$. Also, T3=T1+T2, $\Rightarrow \delta_3=2\delta_1$.
Hence, $\delta_m=6\delta_1$. The restoring force acting on m is due to spring i.e T1 and its magnitude is $k\delta_1=k\delta_m/6$.

Therefore, the time period is $$2\pi\sqrt{\frac{6m}{k}}$$. Looks correct?

Thanks a lot ehild and Chet! :)

For the three tensions, I get:

T₂=kδ₂
T₃=kδ₃
T₁=k(δ_m-δ₁)

Therefore, I get:
δ₂=δ_m-δ₁=δ_m-δ₂-2δ₃
δ₃=δ2+δ_m-δ₁=δ_m-2δ₃

Therefore, I get:
δ₃=δ_m/3
δ₂=δ_m/6
δ₁=5δ_m/6
δ_m-δ₁=δ_m/6

This gives the same final result for the tension T₁ of the wire on the mass, but the intermediate results differ.