How Do You Determine Moments of a 3D Model?

[jeluu9]

Homework Statement

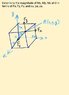
(See pic attachment)

Homework Equations

Moment/Torque = Force * d (Force arm)

The Attempt at a Solution

I have so far
Mx = Fz * ya
My = Fx * za
Mz = -Fx * ya

How I got these answers is by looking at the cube from the component's axis and whether or not it produces a torque. I am following what I observed the professor doing but not sure about why or how one knows how to do this. Please help!

with the coordinate system being CCW is (+) and (+) xyz based on the "left-hand rule"

 

[Chestermiller]

Hi jeluu9. Welcome to Physics Forums!

There should be two terms in each of these equations, and you already have one of the terms written correctly. Try to figure out what the missing term in each equation is.

Have you learned yet about taking the cross product of two vectors, if the vectors are expressed in cartesian component form?

Chet