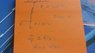How do you determine the function of a spring in terms of k?

[drummerscott]

Homework Statement

*See Attachment*

The problem states to find "y" which I'm assuming is the change in distance from the original point marked "y".

Homework Equations

Hooke's Law

The Attempt at a Solution

I'm pretty sure the change in Y is -0.1in

P=-ky
y=p/-k
y=-0.1

I have no idea how to express things as a function of k (second part of the question)

Thanks!

 

[Tomer]

Maybe it's clear for others, but I find the question totally vague.

 

[drummerscott]

Yeah...that is why I'm quite confused. This isn't for physics either, this is "introductory" homework for strength of materials...