How Do You Graphically Add Vectors A and B in Coordinate Plane?

[nike]

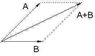
This question is about vectors. It said that add following vectors A=9 along the positive x-axis and B= 12 45 degrees postive axis?

this is how I did it. I graphed the B, but I don't know where to put the A, can someone explain this problem to me.
thanx.

 

[mukundpa]

From the end point of B draw A along x axis and use traingle law.

 

[nike]

I still don't get the right answer when i do that.

 

[mathmike]

when you say b=12 45 degrees positive axis, do you mean positive x-axis

 

[nike]

yes. that's what i meant.

 

[HallsofIvy]

I presume that you have already drawn B at 45 degrees to the x-axis and 12 units long. Now, starting at the tip of the B vector, draw the A vector parallel to the x-axis and 9 units long. Finally, draw the vector from the beginning of B to the tip of A. Measure its angle and length.

As mukundpa said, you can also do this using trig functions. Your picture should show you a triangle with two sides of length 12 and 9. If you look closely at your triangle you should see that the angle at top (the tip of B) has measure 180- 45= 135 degrees (the angle from the horizontal side to B extended is 45 degrees). You can find the length of the other side of the triangle by using the cosine law: C²= 9²+ 12²- 2(9)(12)cos(135)= 81+ 144- 216(-√(2)/2)=225+ 108√(2). Now you could use the sine law to find the angle inside the triangle at the start of B and then subtract that from 45 degrees to find the angle the resultant vector makes with the horizontal.

An even simpler way to do this is to use "components". B has length 12 and makes an angle 45 degrees with the x-axis. sin(45)= cos(45)= √(2)/2 so the two legs of the triangle with B as hypotenuse both have length 6√(2). The x and y components of B are both 6√(2). You can write B as 6√(2)i+ 6√(2)j where i and j are the "unit" vectors in the x and y directions. A has length 9 and only goes along the x-axis so it can be written 9i+ 0j. The sum of A and B is (9+ 6√(2))i+ 6√(2)j. Now you could use the Pythagorean theorem to find the length of A+ B and arctan(6√(2)/(9+6√(2)) to find the angle.

 

[sinochef]

give u a picture

I drew the picture. (attachment)