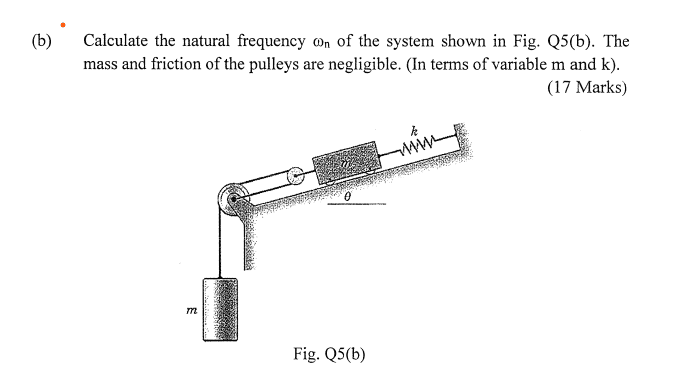
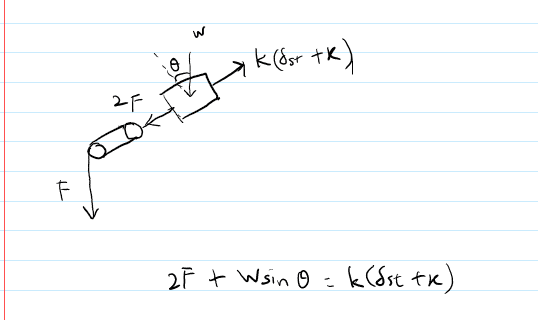SUMMARY
The discussion focuses on expressing the natural frequency ωₙ in terms of mass (m) and stiffness (k) within a pulley system. Participants emphasize the use of Newton's laws and free body diagrams to analyze the forces acting on the masses. A key conclusion is that the natural frequency can be derived from the relationship ω² = k/μ, where μ represents the effective mass in the system. Additionally, energy methods are suggested as a simpler alternative to derive the same results.
PREREQUISITES
- Understanding of Newton's laws of motion
- Familiarity with free body diagrams
- Knowledge of energy conservation principles
- Basic concepts of oscillatory motion and natural frequency
NEXT STEPS
- Study the derivation of natural frequency in mechanical systems
- Learn about free body diagram techniques for multi-body systems
- Explore energy methods in dynamics for solving oscillatory problems
- Investigate the role of generalized coordinates in mechanical systems
USEFUL FOR
Mechanical engineers, physics students, and anyone interested in dynamics and oscillatory systems will benefit from this discussion.