Atem
- 6
- 0
- Homework Statement
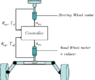
- i have a steering wheel mounted on an electric motor, and i want to stop the driver from going beyond a certain angle. i can read the torque applied by the driver, and the steering wheel angular velocity as well. how can i stop the steering wheel, without sending it harshely in the opposite direction?
- Relevant Equations
- torque = MOI * acceleration (MOI : moment of inertia)
Problem Statement: i have a steering wheel mounted on an electric motor, and i want to stop the driver from going beyond a certain angle. i can read the torque applied by the driver, and the steering wheel angular velocity as well. how can i stop the steering wheel, without sending it harshely in the opposite direction?
Relevant Equations: torque = MOI * acceleration (MOI : moment of inertia)
...
Relevant Equations: torque = MOI * acceleration (MOI : moment of inertia)
...